Dual representations of polynomial modules with applications to partial differential equations

$$ \begin{gather*} \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 g}{\partial x \partial y} = 0 \\ \frac{\partial^2 f }{\partial y \partial z } + \frac{\partial^2 g}{\partial z^2} = 0 \\ \frac{\partial^3 f }{\partial x^2 \partial z } + \frac{\partial^3 g}{\partial z \partial y \partial w} = 0 \end{gather*} $$

Marc Härkönen
PhD dissertation defense,
Apr 15 2022

Example

$$ I = (x_1^2, x_1 x_2) \subset R = \mathbb{Q}[x_1, x_2] $$

Primary decomposition $ I = (x_1) \cap (x_1^2, x_2)$.
"Differential" primary decomposition $$ I = \left\{ f \in R \colon f \text{ vanishes on the line $x_1=0$ and } \frac{\partial f}{\partial x_1} \text{ vanishes at the origin} \right\}$$

Example

$$ I = (x_1^2, x_1 x_2) \subset R = \mathbb{Q}[x_1, x_2] $$

Primary decomposition $ I = (x_1) \cap (x_1^2, x_2)$.
"Differential" primary decomposition $$ \begin{aligned} I = \{ f \in R \colon f \text{ vanishes on the line $x_1=0$ and }& \\ \frac{\partial f}{\partial x_1} \text{ vanishes at the origin} &\} \end{aligned}$$

$$ \frac{\partial^2 \phi}{\partial z_1^2} = \frac{\partial^2 \phi}{\partial z_1 \partial z_2} = 0 $$

Find $ \phi(z_1,z_2) \colon \RR^2 \to \CC$ satisfying the above

Example

$$ I = (x_1^2, x_1 x_2) \subset R = \mathbb{Q}[x_1, x_2] $$

Primary decomposition $ I = (x_1) \cap (x_1^2, x_2)$.
"Differential" primary decomposition $$ \begin{aligned} I = \{ f \in R \colon f \text{ vanishes on the line $x_1=0$ and }& \\ \frac{\partial f}{\partial x_1} \text{ vanishes at the origin} &\} \end{aligned}$$

$$ \frac{\partial^2 \phi}{\partial z_1^2} = \frac{\partial^2 \phi}{\partial z_1 \partial z_2} = 0 $$

Find $ \phi(z_1,z_2) \colon \RR^2 \to \CC$ satisfying the above

Solution: $\phi(z_1,z_2) = \psi(z_2) + c_1 z_1$,

$c_1 \in \CC,~~\psi(z_2) \colon \RR \to \CC$ differentiable.

Example

$$ I = (x_1^2, x_1 x_2) \subset R = \mathbb{Q}[x_1, x_2] $$

Primary decomposition $ I = (x_1) \cap (x_1^2, x_2)$.
"Differential" primary decomposition $$ \begin{aligned} I = \{ f \in R \colon f \text{ vanishes on the line $x_1=0$ and }& \\ \frac{\partial f}{\partial x_1} \text{ vanishes at the origin} &\} \end{aligned}$$

$$ \frac{\partial^2 \phi}{\partial z_1^2} = \frac{\partial^2 \phi}{\partial z_1 \partial z_2} = 0 $$

Find $ \phi(z_1,z_2) \colon \RR^2 \to \CC$ satisfying the above

Solution: $\phi(z_1,z_2) = \psi(z_2) + c_1 z_1$,

$c_1 \in \CC,~~\psi(z_2) \colon \RR \to \CC$ differentiable.

Dualities at two levels

ideals and their differential equations,
differential equations and their solutions

Gröbner duality

$$ R = \KK[x_1,\dotsc,x_n], \qquad p \in \KK^n $$

$$ \begin{aligned} \partial_i \colon R &\to \KK \\ f &\mapsto \partial_i \bullet f = \frac{\partial f}{\partial x_i}(p). \end{aligned} $$

$$W_{\KK} := \KK[\partial_1,\dotsc,\partial_n], \qquad \partial^\alpha \bullet f = \frac{\partial^{|\alpha|} f}{\partial x^\alpha}(p)$$

A $\KK$-vector space
A right $R$-module: $(Dg) \bullet f := D \bullet (gf)$

$$W_{\KK} := \KK[\partial_1,\dotsc,\partial_n], \qquad \partial^\alpha \bullet f = \frac{\partial^{|\alpha|} f}{\partial x^\alpha}(p)$$

A $\KK$-vector space
A right $R$-module: $(Dg) \bullet f := D \bullet (gf)$

Definition

The dual space of $I \subseteq R$ at the point $p$ is $$ I^\perp = \{ D \in W_\KK \colon D \bullet f = 0 \text{ for all } f \in I \}$$ For $\Lambda \subseteq \KK[\partial]$, we have a set of polynomial solutions $$ \Lambda^\perp = \{f \in R \colon D \bullet f = 0 \text{ for all } D \in \Lambda \}$$

$$W_{\KK} := \KK[\partial_1,\dotsc,\partial_n], \qquad \partial^\alpha \bullet f = \frac{\partial^{|\alpha|} f}{\partial x^\alpha}(p)$$

A $\KK$-vector space
A right $R$-module: $(Dg) \bullet f := D \bullet (gf)$

Definition

Theorem (Gröbner)

Let $p \in \KK^n$, $\mm = (x_1 - p_1, \dotsc, x_n - p_n)$. There is a bijection between $\mm$-primary ideals in $R$ and finite dimensional right $R$-modules in $W_\KK$.

Local dual spaces

Suppose $\mm \subset R$ is an arbitrary maximal ideal, $\kappa(\mm) = R/\mm$ the residue field.

$$ \begin{aligned} \partial_i \colon R &\to \kappa(\mm) \\ f &\mapsto \partial_i \bullet f = \frac{\partial f}{\partial x_i} \mod{\mm} \end{aligned} $$

$$W_{\kappa(\mm)} := \kappa(\mm)[\partial_1,\dotsc,\partial_n], \qquad \partial^\alpha \bullet f = \frac{\partial^{|\alpha|} f}{\partial x^\alpha} \mod{\mm}$$

A $\kappa(\mm)$-vector space
A right $R$-module: $(Dg) \bullet f := D \bullet (gf)$

$$W_{\kappa(\mm)} := \kappa(\mm)[\partial_1,\dotsc,\partial_n], \qquad \partial^\alpha \bullet f = \frac{\partial^{|\alpha|} f}{\partial x^\alpha} \mod{\mm}$$

A $\kappa(\mm)$-vector space
A right $R$-module: $(Dg) \bullet f := D \bullet (gf)$

Definition

The local dual space of $I \subseteq R$ at the $\mm$ is $$ D_\mm[I] = \{ D \in W_{\kappa(\mm)} \colon D \bullet f = 0 \text{ for all } f \in I \}$$ For $\Lambda \subseteq W_{\kappa(\mm)}$, we have a set of polynomial solutions $$ I_\mm[\Lambda] = \{f \in R \colon D \bullet f = 0 \text{ for all } D \in \Lambda \}$$ If $\Lambda \subseteq W_{\kappa(\pp)}$ is a $\kappa(\pp)$-vector space and a right $R$-module, we say that $\Lambda$ is a local dual space.

$$W_{\kappa(\mm)} := \kappa(\mm)[\partial_1,\dotsc,\partial_n], \qquad \partial^\alpha \bullet f = \frac{\partial^{|\alpha|} f}{\partial x^\alpha} \mod{\mm}$$

A $\kappa(\mm)$-vector space
A right $R$-module: $(Dg) \bullet f := D \bullet (gf)$

Definition

Theorem

Let $\mm$ be a maximal ideal. We have bijections

$\mm$-primary ideals in $R$ $\leftrightarrow$ finite dimensional local dual spaces in $W_{\kappa(\mm)}$
$\mm$-closed ideals in $R$ $\leftrightarrow$ local dual spaces in $W_{\kappa(\mm)}$

$I \subseteq R$ is $\mm$-closed if $I_\mm \cap R = I$.

Example

$R = \RR[x,y], \qquad \mm = (x-y, y^2+1)$ $$ I = (2xy-y^2+1, x^2 + 1) $$ $$ D_{\mm}[I] = \Span_{\kappa(\mm)}\{ 1, \partial_y \} $$

$\Lambda = \langle \partial_x^2 + \partial_x\partial_y,\,\partial_y^2 \rangle$ $ = \Span_{\kappa(\mm)}\{1,\,\partial_x,\,\partial_y,\,\partial_y^2,\,\partial_x^2 + \partial_x\partial_y\}$ $$ I_{\mm}[\Lambda] = ((x-y)^3, (y^2+1)^2 + 4(x-y)^2, (y^2+1)(x^2-2xy-1)-4(x-y)^2) $$

Some properties

$I$ is an arbitrary ideal
$ D_{\kappa(\mm)}[I] = D_{\kappa(\mm)}[I_\mm \cap R] $

Some properties

$I$ is an arbitrary ideal
$ D_{\kappa(\mm)}[I] = D_{\kappa(\mm)}[I_\mm \cap R] $

$I$ is an ideal if and only if $D_\mm[I]$ is a local dual space
$\Lambda$ is a local dual space if and only if $I_\mm[\Lambda]$ is an ideal.

Some properties

$I$ is an arbitrary ideal
$ D_{\kappa(\mm)}[I] = D_{\kappa(\mm)}[I_\mm \cap R] $

$I$ is an ideal if and only if $D_\mm[I]$ is a local dual space
$\Lambda$ is a local dual space if and only if $I_\mm[\Lambda]$ is an ideal.

$$I \subseteq J \implies D_\mm[I] \supseteq D_\mm[J] \qquad \Lambda \subseteq \Xi \implies I_\mm[\Lambda] \supseteq I_\mm[\Xi] $$

Some properties

$I$ is an arbitrary ideal
$ D_{\kappa(\mm)}[I] = D_{\kappa(\mm)}[I_\mm \cap R] $

$I$ is an ideal if and only if $D_\mm[I]$ is a local dual space
$\Lambda$ is a local dual space if and only if $I_\mm[\Lambda]$ is an ideal.

$$I \subseteq J \implies D_\mm[I] \supseteq D_\mm[J] \qquad \Lambda \subseteq \Xi \implies I_\mm[\Lambda] \supseteq I_\mm[\Xi] $$

If $I$, $J$ ideals, $\Lambda, \Xi$ local dual spaces, then $$ \begin{aligned} D_{\mm}[I \cap J] = D_{\mm}[I] + D_{\mm}[J] && D_{\mm}[I + J] = D_{\mm}[I] \cap D_{\mm}[J] \\ I_{\mm}[\Lambda \cap \Xi] = I_{\mm}[\Lambda] + I_{\mm}[\Xi] && I_{\mm}[\Lambda + \Xi] = I_{\mm}[\Lambda] \cap D_{\mm}[\Xi] \end{aligned} $$

Some properties

$I$ is an arbitrary ideal
$ D_{\kappa(\mm)}[I] = D_{\kappa(\mm)}[I_\mm \cap R] $

$I$ is an ideal if and only if $D_\mm[I]$ is a local dual space
$\Lambda$ is a local dual space if and only if $I_\mm[\Lambda]$ is an ideal.

$$I \subseteq J \implies D_\mm[I] \supseteq D_\mm[J] \qquad \Lambda \subseteq \Xi \implies I_\mm[\Lambda] \supseteq I_\mm[\Xi] $$

$$D_\mm[\mm^k] = \{ D \in W_{\kappa(\mm)} \colon \deg(D) < k \}$$

Non maximal primes

Let $\pp \subset R = \KK[x_1,\dotsc,x_n]$ be a prime.
Let $\tt = \{x_{i_1}, \dotsc, x_{i_d}\}$ denote a maximal set of algebraically independent variables in $R/\pp$,
let $\yy = \{x_{j_1}, \dotsc, x_{j_c}\}$ denote the rest.
Relabel the variables so that $R = \KK[\tt, \yy]$.

Denote by $\cdot^\ttt$ the localization at the multiplicatively closed set $\KK[\tt] \setminus \{0\}$.

$$ R^\ttt = \KK(\tt)[\yy] $$

$ \pp^\ttt $ is a maximal ideal in $R^\ttt$

$ \kappa(\pp^\ttt) = R^\ttt/\pp^\ttt $ is isomorphic to the residue field $ \kappa(\pp) = (R/\pp)_\pp $

$$ R^\ttt = \KK(\tt)[\yy] $$

$ \pp^\ttt $ is a maximal ideal in $R^\ttt$

$ \kappa(\pp^\ttt) = R^\ttt/\pp^\ttt $ is isomorphic to the residue field $ \kappa(\pp) = (R/\pp)_\pp $

Study the local dual space $$ D_{\pp^\ttt}[I^\ttt] \subseteq W_{\kappa(\pp^\ttt)}$$

Warning: if $D \in W_{\kappa(\pp^\ttt)}$, then $$ D = \sum_\alpha c_\alpha \partial_\yy^\alpha $$ where $c_\alpha \in \kappa(\pp)$.
There are no $\partial_\tt$ variables!

Theorem

$\pp \in R$ prime, $\tt$ a maximal set of independent variables over $\pp$.
There are bijections

$\pp$-primary ideals $I \subset R$ $\leftrightarrow$ finite dimensional local dual spaces $\Lambda \subseteq W_{\kappa(\pp^\ttt)}$
$\pp$-closed ideals $I \subset R$ $\leftrightarrow$ local dual spaces $\Lambda \subseteq W_{\kappa(\pp^\ttt)}$,

given by $$ \begin{aligned} I &\mapsto D_{\pp^\ttt}[I^\ttt] \\ \Lambda &\mapsto I_{\pp^\ttt}[\Lambda] \cap R \end{aligned} $$

Example

$R = \QQ[t,x,y]$
$I = (x^2, y-tx)$ is a $\pp = (x,y)$-primary ideal.

The set $\{t\}$ is a maximal set of independent variables.
$\kappa(\pp) = \QQ(t)$

$$ D_{\pp^\ttt}[I^\ttt] = \Span_{\kappa(\pp)} \left\{ 1,~\partial_y,~\partial_y^2 - \frac{2}{t}\partial_x,~\partial_y^3+\frac{6}{t}\partial_x\partial_y \right\} $$

$ = \Span_{\kappa(\pp)} \left\{ 1,~\partial_y,~t\partial_y^2 - 2\partial_x,~t\partial_y^3+6\partial_x\partial_y \right\} $

Definition

Let $I$ be $\pp$-primary, $\tt$ a maximal independent set.
A set of Noetherian operators is a finite set $\DD \subseteq W_{\kappa(\pp^\ttt)}$ such that $$ \Span_{\kappa(\pp)} \DD = D_{\pp^\ttt}[I^\ttt] $$

Theorem

$\DD$ is a set of Noetherian operators for $I$ if and only if $$ I = \{ f \in R \colon D \bullet f = 0 \text{ for all } D \in \DD \} $$

Example

$ I = (y^4, xy^3, x^3y^2)$ $ = (y^2) \cap (x^3,\,y^4,\,x^3y^2)$

Noetherian operators:
$\pp_1 = (y), \DD = \{1,\partial_y\}$

$\pp_2 = (x,y)$ $$\begin{aligned}\DD = \{& 1, \partial_x, \partial_x^2, \\ & \partial_y, \partial_y\partial_x, \partial_y\partial_x^2, \\ & \partial_y^2, \partial_y^2\partial_x, \partial_y^2\partial_x^2, \partial_y^3 \} \end{aligned}$$

Example

$ I = (y^4, xy^3, x^3y^2)$ $ = (y^2) \cap (x^3,\,y^4,\,x^3y^2)$

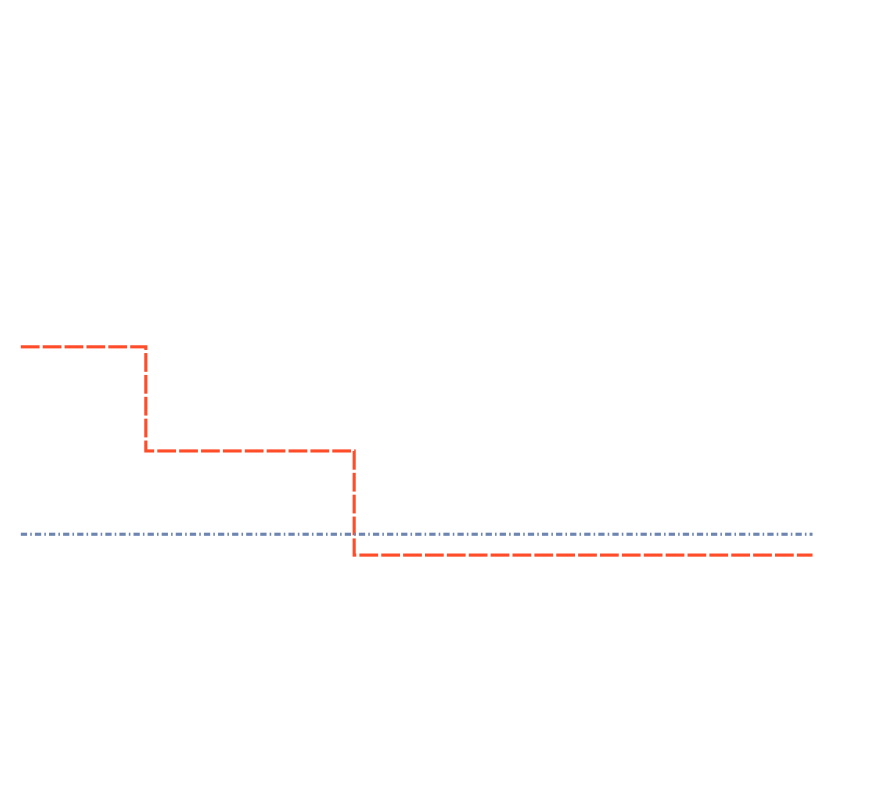
$D_{(x,y)}[I]$ $D_{(x,y)}[(y^2)]$

Example

$ I = (y^4, xy^3, x^3y^2)$ $ = (y^2) \cap (x^3,\,y^4,\,x^3y^2)$

~~Noetherian operators:~~
$\pp_1 = (y), \DD = \{1,\partial_y\}$

$\pp_2 = (x,y)$ $$\begin{aligned}\DD = \{& \partial_y^2, \partial_y^2\partial_x, \partial_y^2\partial_x^2, \partial_y^3 \} \end{aligned}$$

$D_{(x,y)}[I]$ $D_{(x,y)}[(y^2)]$

Arbitrary ideals

Let $I \subseteq R$, $\pp$ an associated prime, $\tt$ a maximal set of independent variables.

Let $J = I_\pp \cap R$ be the $\pp$-closure of $I$.

$$ J = Q \cap (J \colon \pp^\infty) $$

$$ D_{\pp^\ttt}[J^\ttt] = D_{\pp^\ttt}[Q^\ttt] + D_{\pp^\ttt}[(J \colon \pp^\infty)^\ttt] $$

$$ D_{\pp^\ttt}[I^\ttt] = D_{\pp^\ttt}[Q^\ttt] + D_{\pp^\ttt}[(I \colon \pp^\infty)^\ttt] $$

$ \implies $ $ \frac{D_{\pp^\ttt}[I^\ttt]}{D_{\pp^\ttt}[(I \colon \pp^\infty)^\ttt]} $ is a finite dimensional $\kappa(\pp)$-vector space.

Arbitrary ideals

Let $I \subseteq R$, $\pp$ an associated prime, $\tt$ a maximal set of independent variables.

Definition

The excess dual space of $I$ at $\pp$ is the finite dimensional $\kappa(\pp)$-vector space $ \frac{D_{\pp^\ttt}[I^\ttt]}{D_{\pp^\ttt}[(I \colon \pp^\infty)^\ttt]} $.

Definition

Let $I \subseteq R$ be an ideal.
For each $\pp \in \Ass(I)$ let $\tt_\pp$ be a maximal set of independent variables over $\pp$.

A differential primary decomposition is a list of triples $$ \{(\pp, \tt_\pp, \DD_\pp) \}_{\pp \in \Ass(I)} $$ such that the images of $\DD_\pp \in W_{\kappa(\pp^\ttp)}$ span the excess dual space.

Definition

Let $I \subseteq R$ be an ideal.
For each $\pp \in \Ass(I)$ let $\tt_\pp$ be a maximal set of independent variables over $\pp$.

A differential primary decomposition is a list of triples $$ \{(\pp, \tt_\pp, \DD_\pp) \}_{\pp \in \Ass(I)} $$ such that the images of $\DD_\pp \in W_{\kappa(\pp^\ttp)}$ span the excess dual space.

Proposition

$ I = \{ f \in R \colon D \bullet f = 0 \text{ for all } D \in \DD_{\mathfrak{p}},\, \pp \in \Ass(I) \} $

Definition

Let $I \subseteq R$ be an ideal.
For each $\pp \in \Ass(I)$ let $\tt_\pp$ be a maximal set of independent variables over $\pp$.

A differential primary decomposition is a list of triples $$ \{(\pp, \tt_\pp, \DD_\pp) \}_{\pp \in \Ass(I)} $$ such that the images of $\DD_\pp \in W_{\kappa(\pp^\ttp)}$ span the excess dual space.

Proposition

$ I = \{ f \in R \colon D \bullet f = 0 \text{ for all } D \in \DD_{\mathfrak{p}},\, \pp \in \Ass(I) \} $

Theorem

$ \{(\pp, \tt_\pp, \DD_\pp) \}_{\pp \in \Ass(I)} $ is a differential primary decomposition if and only if, for each $\pp \in \Ass(I)$ $$ I_\pp \cap R = \{ f \in R \colon D \bullet f = 0 \text{ for all } D \in \DD_{\mathfrak{q}},\, \pp \supseteq {\mathfrak{q}} \in \Ass(I) \} $$

Example

Let $I = (x(y-z), x^2z, x^3)$: a plane $x=0$ with an embedded line $x=y-z = 0$ with a further embedded point at the origin.

$$ \begin{Bmatrix} ((x), & \{y,z\}, & \{1\}), \\ ((x,y-z), & \{z\}, & \{\partial_x\}), \\ ((x,y,z), & \emptyset, & \{\partial_x^2\}) \end{Bmatrix} $$


Macaulay2, version 1.19.1.1
i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : I = ideal(x*y-x*z,x^2*z,x^3);
i4 : differentialPrimaryDecomposition I

o4 = {{ideal x, {| 1 |}}, {ideal (y - z, x), {| dx |}}, {ideal (z, y, x), {| dx^2 |}}}

o4 : List

Example

Let $I = (x(y-z), x^2z, x^3)$: a plane $x=0$ with an embedded line $x=y-z = 0$ with a further embedded point at the origin.

$$ \begin{Bmatrix} ((x), & \{y,z\}, & \{1\}), \\ ((x,y-z), & \{z\}, & \{\partial_x\}), \\ ((x,y,z), & \emptyset, & \{\partial_x^2\}) \end{Bmatrix} $$


Macaulay2, version 1.19.1.1
i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : I = ideal(x*y-x*z,x^2*z,x^3);
i4 : differentialPrimaryDecomposition I

o4 = {{ideal x, {| 1 |}}, {ideal (y - z, x), {| dx |}}, {ideal (z, y, x), {| dx^2 |}}}

o4 : List

J. Chen, Y. Cid-Ruiz, M. Härkönen, R. Krone, and A. Leykin, Noetherian operators in Macaulay2, 2021. arXiv:2101.01002.
J. Chen, M. Härkönen, R. Krone, and A. Leykin, “Noetherian operators and primary decomposition,” J. Symbolic Comput., vol. 110, 2022.

Modules

Everything translates to $R$-submodules $U \subseteq R^k$!

Modules

$ \begin{gathered} \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 g}{\partial x \partial y} = 0 \\ \frac{\partial^2 f }{\partial y \partial z } + \frac{\partial^2 g}{\partial z^2} = 0 \\ \frac{\partial^3 f }{\partial x^2 \partial z } + \frac{\partial^3 g}{\partial z \partial y \partial w} = 0 \end{gathered} $

Everything translates to $R$-submodules $U \subseteq R^k$!

If $D \in W_{\kappa(\mm)}^k$, $f \in R^k$, then

$ D \bullet f = \sum_{i=1}^k D_i \bullet f_i $

$$ \begin{aligned} U &\mapsto D_{\pp^\ttt}[U^\ttt] \subseteq (W_{\kappa(\pp^\ttt)})^k \\ \Lambda &\mapsto I_{\pp^\ttt}[\Lambda] \cap R^k \end{aligned}$$

Example

Let $$ U = \im_R \begin{bmatrix}0 & x^2 & xy^2 \\ x & 0 & -2y^2 \end{bmatrix} $$

Example

Let $$ U = \im_R \begin{bmatrix}0 & x^2 & xy^2 \\ x & 0 & -2y^2 \end{bmatrix} $$


i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : U = image matrix {{0, x^2, x*y^2}, {x, 0, -2*y^2}}

o3 = image | 0 x2 xy2  |
					 | x 0  -2y2 |

														 2
o3 : R-module, submodule of R

i4 : differentialPrimaryDecomposition U

o4 = {{ideal x, {| 1 |, | 2dx |}}, {ideal (y, x), {| dx |, |  0 |}}}
								 | 0 |  |  1  |                    |  0 |  | dy |

Example

Let $$ U = \im_R \begin{bmatrix}0 & x^2 & xy^2 \\ x & 0 & -2y^2 \end{bmatrix} $$


i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : U = image matrix {{0, x^2, x*y^2}, {x, 0, -2*y^2}}

o3 = image | 0 x2 xy2  |
					 | x 0  -2y2 |

														 2
o3 : R-module, submodule of R

i4 : differentialPrimaryDecomposition U

o4 = {{ideal x, {| 1 |, | 2dx |}}, {ideal (y, x), {| dx |, |  0 |}}}
								 | 0 |  |  1  |                    |  0 |  | dy |

$\left[\begin{smallmatrix}f \\ g \end{smallmatrix} \right] \in R^2$ belongs to $U$ if and only if

$f$ and $2\frac{\partial f}{\partial x} + g$ vanish on the line $x = 0$
$\frac{\partial f}{\partial x}$ and $\frac{\partial g}{\partial y}$ vanish at the point $x = y = 0$.

Example

Let $$ U = \im_R \begin{bmatrix}0 & x^2 & xy^2 \\ x & 0 & -2y^2 \end{bmatrix} $$


i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : U = image matrix {{0, x^2, x*y^2}, {x, 0, -2*y^2}}

o3 = image | 0 x2 xy2  |
					 | x 0  -2y2 |

														 2
o3 : R-module, submodule of R

i4 : differentialPrimaryDecomposition U

o4 = {{ideal x, {| 1 |, | 2dx |}}, {ideal (y, x), {| dx |, |  0 |}}}
								 | 0 |  |  1  |                    |  0 |  | dy |

$\left[\begin{smallmatrix}f \\ g \end{smallmatrix} \right] \in R^2$ belongs to $U$ if and only if

$f$ and $2\frac{\partial f}{\partial x} + g$ vanish on the line $x = 0$
$\frac{\partial f}{\partial x}$ and $\frac{\partial g}{\partial y}$ vanish at the point $x = y = 0$.

J. Chen and Y. Cid-Ruiz, “Primary decomposition of modules: A computational differential approach,” Journal of Pure and Applied Algebra, 2022.
R. Ait El Manssour, M. Härkönen, and B. Sturmfels, “Linear PDE with constant coefficients,” Glasgow Mathematical Journal, First View, 2021.

PDE

Let $R = \CC[x_1,\dotsc,x_n] = \CC[\partial_{z_1}, \dotsc, \partial_{z_n}]$.

A $\ell \times k$ matrix with entries in $R$ describes a system of $\ell$ linear homogeneous PDE with constant coefficients

Its solution is an unknown function
$v(z_1,\dotsc,z_n) \colon \RR^n \to \CC^k$

PDE

Let $R = \CC[x_1,\dotsc,x_n] = \CC[\partial_{z_1}, \dotsc, \partial_{z_n}]$.

A $\ell \times k$ matrix with entries in $R$ describes a system of $\ell$ linear homogeneous PDE with constant coefficients

Its solution is an unknown function
$v(z_1,\dotsc,z_n) \colon \RR^n \to \CC^k$

Example

$\ell = 3, k = 2 $

$ M = \begin{bmatrix} 0 & x_1 \\ x_1^2 & 0 \\ x_1 x_2^2 & -2x_2^2 \end{bmatrix} $

$ M \bullet v = 0 $ means finding $ v(z_1,z_2) \colon \RR^2 \to \CC^2 $ such that $$ \begin{gathered} \partial_{z_1} \bullet v_2 = 0 \\ \partial_{z_1}^2 \bullet v_1 = 0 \\ \partial_{z_1}\partial_{z_2}^2 \bullet v_1 - 2 \partial_{z_2}^2 \bullet v_2 = 0 \end{gathered} $$

Let $\ff$ be an $R$-module of functions, $M \in R^{\ell \times k}$.

The solution space $$ \Sol_\ff(M) = \{v \in \ff^k \colon M \bullet v = 0 \} $$ is an $R$-module.

It only depends on the module $U = \im_R M^T \subseteq R^k$

$\ff = C_c^\infty$

Theorem (Malgrange 1960)

The set of compactly supported smooth functions is an injective $R$-module

$\ff = C_c^\infty$

Theorem (Malgrange 1960)

The set of compactly supported smooth functions is an injective $R$-module

$$ R^{k'} \xrightarrow{S} R^k \xrightarrow{M} R^\ell $$

$$ R^{k'} \otimes_R C_c^\infty \xrightarrow{S \otimes 1} R^k \otimes_R C_c \xrightarrow{M \otimes 1} R^\ell \otimes_R C_c^\infty $$

$$ (C_c^\infty)^{k'} \xrightarrow{S} (C_c^\infty)^k \xrightarrow{M} (C_c^\infty)^\ell $$

$$\Sol_{C_c^\infty}(M) = \im_{C_c^\infty}(S) = \{ S \bullet u \colon u \in (C_c^\infty)^{k'} \} $$

$\ff = C^\infty$ or $\DD'$

Example

$ v'''(z) - 3v''(z) + 4 = 0 $

Characteristic polynomial
$ x^3 - 3x^2 - 4 = 0 $

Characteristic polynomial
$ (x-2)^2(x+1) = 0 $

Solutions
$ e^{2z}, ze^{2z}$
$ e^{-z} $

Local dual spaces $$\begin{aligned} x=2&: & \langle 1, \partial_x \rangle\\ x=-1&: & \langle 1 \rangle \end{aligned}$$

$\ff = C^\infty$ or $\DD'$

Example

$ v'''(z) - 3v''(z) + 4 = 0 $

Characteristic polynomial
$ (x-2)^2(x+1) = 0 $

Solutions
$ e^{2z}, ze^{2z}$
$ e^{-z} $

Local dual spaces $$\begin{aligned} x=2&: & \langle 1, \partial_x \rangle\\ x=-1&: & \langle 1 \rangle \end{aligned}$$

Theorem

Let $U \subseteq R^k$ be an $R$-submodule, $\pp$ a prime.
The operator $D = D(x,\partial_x) \in D_{\pp^\ttt}[I^\ttt]$ if and only if $$ D(x_0, z) \exp(x_0^T \cdot z) \in \Sol_\ff (U) $$ for (almost) all $x_0 \in V(\pp)$.

Theorem (improved Ehrenpreis-Palamodov)

Let $\{(\pp, \tt_\pp, \DD_\pp)\}_{\pp \in \Ass(R^k/U)}$ be a differential primary decomposition for the $R$-submodule $U \subseteq R$. All distributional solutions $u \in \Sol_{\DD'}(U)$ are of the form $$ u(z) = \sum_{\pp \in \Ass(R^k/U)} \sum_{D \in \DD_\pp} \int_{V(\pp)} D(x,z) \exp(x^T \cdot z)\,\mathrm{d}\mu_{\pp,D}(x) $$ for a suitable set of measures $\mu_{\pp,D}$.

Example

$$ M = \begin{bmatrix} 0 & x_1 \\ x_1^2 & 0 \\ x_1 x_2^2 & -2x_2^2 \end{bmatrix} $$ $$ U = \im_R M^T $$ Find $v \in \Sol_{\DD'}(M)$

Example

$$ M = \begin{bmatrix} 0 & x_1 \\ x_1^2 & 0 \\ x_1 x_2^2 & -2x_2^2 \end{bmatrix} $$ $$ U = \im_R M^T $$ Find $v \in \Sol_{\DD'}(M)$


i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : U = image matrix {{0, x^2, x*y^2}, {x, 0, -2*y^2}}

o3 = image | 0 x2 xy2  |
					 | x 0  -2y2 |

														 2
o3 : R-module, submodule of R

i4 : solvePDE U

o4 = {{ideal x, {| 1 |, | 2dx |}}, {ideal (y, x), {| dx |, |  0 |}}}
								 | 0 |  |  1  |                    |  0 |  | dy |

Example

$$ M = \begin{bmatrix} 0 & x_1 \\ x_1^2 & 0 \\ x_1 x_2^2 & -2x_2^2 \end{bmatrix} $$ $$ U = \im_R M^T $$ Find $v \in \Sol_{\DD'}(M)$


i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : U = image matrix {{0, x^2, x*y^2}, {x, 0, -2*y^2}}

o3 = image | 0 x2 xy2  |
					 | x 0  -2y2 |

														 2
o3 : R-module, submodule of R

i4 : solvePDE U

o4 = {{ideal x, {| 1 |, | 2dx |}}, {ideal (y, x), {| dx |, |  0 |}}}
								 | 0 |  |  1  |                    |  0 |  | dy |

$$ \begin{aligned} v(z_1,z_2) =& \int_{V(x_1)} \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_1(x) + \int_{V(x_1)} \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_2(x) \\ &+ \int_{V(x_1,x_2)} \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_3(x) + \int_{V(x_1,x_2)} \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_4(x) \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) =& \int_{V(x_1)} \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_1(x) + \int_{V(x_1)} \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_2(x) \\ &+ \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big)c_3 + \int_{V(x_1,x_2)} \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_4(x) \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) =& \int_{V(x_1)} \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_1(x) + \int_{V(x_1)} \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) e^{x_1z_1 + x_2z_2}\,\mathrm{d}\mu_2(x) \\ &+ \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big)c_3 + \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big)c_4 \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) =& \int_{\CC} \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) e^{0z_1+x_2z_2}\,\mathrm{d}\mu_1(x_2) + \int_{\CC} \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) e^{0z_1+x_2z_2}\,\mathrm{d}\mu_2(x_2) \\ &+ \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big)c_3 + \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big)c_4 \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) =& \int_{\CC} \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) e^{x_2z_2}\,\mathrm{d}\mu_1(x_2) + \int_{\CC} \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) e^{x_2z_2}\,\mathrm{d}\mu_2(x_2) \\ &+ \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big)c_3 + \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big)c_4 \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) =& \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) \int_{\CC} e^{x_2z_2}\,\mathrm{d}\mu_1(x_2) + \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) \int_{\CC} e^{x_2z_2}\,\mathrm{d}\mu_2(x_2) \\ &+ \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big)c_3 + \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big)c_4 \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) =& \big(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\big) \phi_1(z_2) + \big(\begin{smallmatrix} 2z_1 \\ 1 \end{smallmatrix}\big) \phi_2(z_2) \\ &+ \big(\begin{smallmatrix} z_1 \\ 0 \end{smallmatrix}\big)c_3 + \big(\begin{smallmatrix} 0 \\ z_2 \end{smallmatrix}\big)c_4 \end{aligned} $$

$$ \begin{aligned} v(z_1,z_2) = \begin{pmatrix} \phi_1(z_2) + 2z_1 \phi_2(z_2) + c_3 z_1 \\ \phi_2(z_2) + c_4z_2 \end{pmatrix} \end{aligned} $$ for some univariate functions $\phi_1,\phi_2 \colon \RR \to \CC$ and complex values $c_3,c_4$.

Example

$$ M = \begin{bmatrix} 0 & x_1 \\ x_1^2 & 0 \\ x_1 x_2^2 & -2x_2^2 \end{bmatrix} $$ $$ U = \im_R M^T $$ Find $v \in \Sol_{\DD'}(M)$


i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : U = image matrix {{0, x^2, x*y^2}, {x, 0, -2*y^2}}

o3 = image | 0 x2 xy2  |
					 | x 0  -2y2 |

														 2
o3 : R-module, submodule of R

i4 : solvePDE U

o4 = {{ideal x, {| 1 |, | 2dx |}}, {ideal (y, x), {| dx |, |  0 |}}}
								 | 0 |  |  1  |                    |  0 |  | dy |

M. Härkönen, J. Hirsch, and B. Sturmfels, Making waves, 2021. arXiv:2111.14045.

Constant rank operators

Let $R = \KK[x_1,\dotsc,x_n]$, where $\KK = \RR$ or $\CC$.
Let $\ff = \DD'$, the space of distributions.
Let $M \in R^{\ell \times k}$ have homogeneous rows.

We say that $M$ has $\KK$-constant rank $r$ if $\rank_\KK M(x) = r$ for all $x \in \KK^m \setminus \{0\}$.

Theorem (controllable-uncontrollable decomposition)

Let $M \in R^{\ell \times k}$ and let $S$ be the syzygy matrix of $M$.
Then there is an operator $M_1$ such that $$ \Sol_\ff(M) = \im_\ff S + \Sol_\ff(M_1) $$ where $\Sol_\ff(M_1)$ contains no compactly supported distributions.

$$ \Sol_\ff(M) = \im_\ff S + \Sol_\ff(M_1) \\ v = S\bullet u + w $$

Theorem

If $M$ has $\KK$-constant rank (where $\KK$ is either $\CC$ or $\RR$), then $M_1$ is $\KK$-elliptic.

$$ \Sol_\ff(M) = \im_\ff S + \Sol_\ff(M_1) \\ v = S\bullet u + w $$

Theorem

If $M$ has $\KK$-constant rank (where $\KK$ is either $\CC$ or $\RR$), then $M_1$ is $\KK$-elliptic.

We say that $M$ is $\KK$-elliptic if $\ker_\KK M(x) = \{0\}$ for all $x \in \KK^m \setminus \{0\}$.

$$ \Sol_\ff(M) = \im_\ff S + \Sol_\ff(M_1) \\ v = S\bullet u + w $$

Theorem

If $M$ has $\KK$-constant rank (where $\KK$ is either $\CC$ or $\RR$), then $M_1$ is $\KK$-elliptic.

We say that $M$ is $\KK$-elliptic if $\ker_\KK M(x) = \{0\}$ for all $x \in \KK^m \setminus \{0\}$.

If $M$ is $\RR$-elliptic, solutions to $M \bullet w = 0$ are smooth.
If $M$ is $\CC$-elliptic, solutions to $M \bullet w = 0$ are polynomials.

$$ \Sol_\ff(M) = \im_\ff S + \Sol_\ff(M_1) \\ v = S\bullet u + w $$

Theorem

If $M$ has $\KK$-constant rank (where $\KK$ is either $\CC$ or $\RR$), then $M_1$ is $\KK$-elliptic.

We say that $M$ is $\KK$-elliptic if $\ker_\KK M(x) = \{0\}$ for all $x \in \KK^m \setminus \{0\}$.

If $M$ is $\RR$-elliptic, solutions to $M \bullet w = 0$ are smooth.
If $M$ is $\CC$-elliptic, solutions to $M \bullet w = 0$ are polynomials.

M. Härkönen, B. Raiță, and L. Nicklasson, Syzygies, constant rank, and beyond, 2021. arXiv:2112.12663.

Conclusion

Algebra

Ideals and modules: generators vs differential primary decomposition
Numerical methods

Analysis

Analytic intuition for solving algebra problems
Examples and counterexamples in analysis

Algebra $\cap$ Analysis

Interesting algebraic objects as PDE
Interesting PDE as algebraic objects

Conclusion

Homework: Solve the PDE

Hint:

needsPackage "NoetherianOperators";
viewHelp(solvePDE)

Algebra

Ideals and modules: generators vs differential primary decomposition
Numerical methods

Analysis

Analytic intuition for solving algebra problems
Examples and counterexamples in analysis

Algebra $\cap$ Analysis

Interesting algebraic objects as PDE
Interesting PDE as algebraic objects

BREAK

Waves