Dual representations of polynomial modules with applications to partial differential equations
Marc Härkönen
Max Planck Institute for Mathematics in the Sciences
NCM 2022,
Aug 20 2022
Example
$$ \phi'''(z)-3\phi'(z)+2\phi(z) = 0 $$
Characteristic polynomial:
$$ x^3-3x+2 = 0 $$
$$ (1-x)^2(x+2) = 0 $$
Solutions
$$ e^z, ze^z, z^{-2z} $$
Example
$$ \phi'''(z)-3\phi'(z)+2\phi(z) = 0 $$
Characteristic polynomial:
$$ (1-x)^2(x+2) = 0 $$
Solutions
$$ e^z, ze^z, z^{-2z} $$
$ I = \langle x^3 - 3x + 2 \rangle \subset R := \CC[x]$
Primary decomposition:
$$ I = \langle (1-x)^2 \rangle \cap \langle x+2 \rangle $$
$I$ is the set of $f \in R$ such that
- $f(1) = 0$
- $ \partial_x f(1) = 0 $
- $ f(-2) = 0 $
Example
$$ \phi'''(z)-3\phi'(z)+2\phi(z) = 0 $$
Characteristic polynomial:
$$ (1-x)^2(x+2) = 0 $$
Solutions
$$ e^z, ze^z, z^{-2z} $$
$ I = \langle x^3 - 3x + 2 \rangle \subset R := \CC[x]$
Primary decomposition:
$$ I = \langle (1-x)^2 \rangle \cap \langle x+2 \rangle $$
$I$ is the set of $f \in R$ such that
- $f(1) = 0$
- $ \partial_x f(1) = 0 $
- $ f(-2) = 0 $
The data $\{(1,1)$, $(\partial_x, 1)$, $(1, 2)\}$ is:
1. the solutions to the PDE $I$;
2. the differential equations of the ideal $I$.
Example
$$ \partial_{z_1}^2 \phi - \partial_{z_2} \phi = 0 \\ \partial_{z_2} \partial_{z_3} \phi = 0 $$
Characteristic polynomials:
$$ x_1^2 - x_2 = 0 \\ x_2x_3 = 0 $$
Solutions
$e^{x_3z_3}, z_1e^{x_3z_3}$ for all $x_3 \in \CC$
$e^{x_1z_1 + x_2z_2 + x_3z_3} $,
where $x \in V(x_1^2 -x_2, x_3)$.
$ I = \langle x_1^2 - x_2, x_2x_3 \rangle \subset R := \CC[x_1,x_2,x_3]$
Primary decomposition:
$$ I = \langle x_1^2, x_2 \rangle \cap \langle x_1^2 - x_2, x_3 \rangle $$
$I$ is the set of $f \in R$ such that
- $f(0,0,x_3) = 0$ for all $x_3 \in \CC$
- $ \partial_{x_1} f(0,0,x_3) = 0 $ for all $x_3 \in \CC$
- $ f(x) = 0 $, when $x \in V(x_1^2 - x_2, x_3)$
Example
$$ \partial_{z_1}^2 \phi - \partial_{z_2} \phi = 0 \\ \partial_{z_2} \partial_{z_3} \phi = 0 $$
Characteristic polynomials:
$$ x_1^2 - x_2 = 0 \\ x_2x_3 = 0 $$
Solutions
$e^{x_3z_3}, z_1e^{x_3z_3}$ for all $x_3 \in \CC$
$e^{x_1z_1 + x_2z_2 + x_3z_3} $,
where $x \in V(x_1^2 -x_2, x_3)$.
$ I = \langle x_1^2 - x_2, x_2x_3 \rangle \subset R := \CC[x_1,x_2,x_3]$
Primary decomposition:
$$ I = \langle x_1^2, x_2 \rangle \cap \langle x_1^2 - x_2, x_3 \rangle $$
$I$ is the set of $f \in R$ such that
- $f(0,0,x_3) = 0$ for all $x_3 \in \CC$
- $ \partial_{x_1} f(0,0,x_3) = 0 $ for all $x_3 \in \CC$
- $ f(x) = 0 $, when $x \in V(x_1^2 - x_2, x_3)$
If $V_1 = V(x_1,x_2)$, $V_2 = V(x_1^2 - x_2, x_3)$,
the data $\{(1,V_1)$, $(\partial_{x_1}, V_1)$, $(1, V_2)\}$ is:
1. the solutions to the PDE $I$;
2. the differential equations of the ideal $I$.
Example
$$ \partial_{z_1}^2 \phi - \partial_{z_2} \phi = 0 \\ \partial_{z_2} \partial_{z_3} \phi = 0 $$
Solutions
$e^{x_3z_3}, z_1e^{x_3z_3}$ for all $x_3 \in \CC$
$e^{x_1z_1 + x_2z_2 + x_3z_3} $,
where $x \in V(x_1^2 -x_2, x_3)$.
Ehrenpreis-Palamodov
Let $V_1 = V(x_1,x_2)$, $V_2 = V(x_1^2 - x_2, x_3)$.
All (smooth/distrbutional) solutions are given by
$$ \phi(z) = \int_{V_1} e^{x_1z_1+x_2z_2+x_3z_3} d\mu_1(x) \\ + z_1 \int_{V_1} e^{x_1z_1+x_2z_2+x_3z_3} d\mu_2(x) \\ + \int_{V_2} e^{x_1z_1 + x_2z_2 + x_3z_3} d\mu_3(x)$$
Example
$$ \partial_{z_1}^2 \phi - \partial_{z_2} \phi = 0 \\ \partial_{z_2} \partial_{z_3} \phi = 0 $$
Solutions
$e^{x_3z_3}, z_1e^{x_3z_3}$ for all $x_3 \in \CC$
$e^{x_1z_1 + x_2z_2 + x_3z_3} $,
where $x \in V(x_1^2 -x_2, x_3)$.
Ehrenpreis-Palamodov
Let $V_1 = V(x_1,x_2)$, $V_2 = V(x_1^2 - x_2, x_3)$.
All (smooth/distrbutional) solutions are given by
$$ \phi(z) = \int_{\CC} e^{x_3z_3} d\mu_1(x_3) \\ + z_1 \int_{\CC} e^{x_3z_3} d\mu_2(x_3) \\ + \int_{V_2} e^{x_1z_1 + x_2z_2 + x_3z_3} d\mu_3(x)$$
Example
$$ \partial_{z_1}^2 \phi - \partial_{z_2} \phi = 0 \\ \partial_{z_2} \partial_{z_3} \phi = 0 $$
Solutions
$e^{x_3z_3}, z_1e^{x_3z_3}$ for all $x_3 \in \CC$
$e^{x_1z_1 + x_2z_2 + x_3z_3} $,
where $x \in V(x_1^2 -x_2, x_3)$.
Ehrenpreis-Palamodov
Let $V_1 = V(x_1,x_2)$, $V_2 = V(x_1^2 - x_2, x_3)$.
All (smooth/distrbutional) solutions are given by
$$ \phi(z) = \psi_1(z_3) + z_1 \psi_2(z_3) \\ + \int_{\CC} e^{x_1z_1 + x_1^2z_2} d\mu_3(x_1)$$
Theorem (Ehrenpreis'54, Palamodov'63)
Let $I \subseteq \CC[x_1,\dotsc,x_n]$ denote a system of PDE. There exists varieties $V_1,\dotsc, V_s$ and polynomials $D_{i,1}, \dotsc, D_{i,t_i}$ such that all distributional solutions $\phi$ are of the form $$ \phi(z) = \sum_{i=1}^s \sum_{j=1}^{t_i} \int_{V_i} D_{i,j}(x,z) \exp(x^T \cdot z)\,\mathrm{d}\mu_{i,j}(x) $$ for a suitable set of measures $\mu_{i,j}$.
Theorem (Ehrenpreis'54, Palamodov'63)
Let $I \subseteq \CC[x_1,\dotsc,x_n]$ denote a system of PDE. There exists varieties $V_1,\dotsc, V_s$ and polynomials $D_{i,1}, \dotsc, D_{i,t_i}$ such that all distributional solutions $\phi$ are of the form $$ \phi(z) = \sum_{i=1}^s \sum_{j=1}^{t_i} \int_{V_i} D_{i,j}(x,z) \exp(x^T \cdot z)\,\mathrm{d}\mu_{i,j}(x) $$ for a suitable set of measures $\mu_{i,j}$.
- $\{V_1,\dotsc, V_s\} = \{V(\pp)\}_{\pp \in \Ass(I)}$
- The polynomials $D_{i,j}$ describe membership in $I$: $$ f \in I \iff D_{i,j}(x,\partial_x) f(x) \in I(V_i), \forall i = 1,\dotsc,s;\,j = 1, \dotsc, t_i. $$
- $\operatorname{amult}(I)$ summands needed Cid-Ruiz, Sturmfels (2021)
We call the data $$\{(V_i, D_{i,j})\}_{i=1,\dotsc,s;\,j=1,\dotsc,t_i}$$ a differential primary decomposition of $I$.
Example
Let $I = (x(y-z), x^2z, x^3)$: a plane $x=0$ with an embedded line $x=y-z = 0$ with a further embedded point at the origin.
$$ \begin{Bmatrix} (V(x), & 1), \\ (V(x,y-z), & \partial_x), \\ (V(x,y,z), & \partial_x^2) \end{Bmatrix} $$
Macaulay2, version 1.20
i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : I = ideal(x*y-x*z,x^2*z,x^3);
i4 : differentialPrimaryDecomposition I
o4 = {{ideal x, {| 1 |}}, {ideal (y - z, x), {| dx |}}, {ideal (z, y, x), {| dx^2 |}}}
o4 : List
Example
Let $I = (x(y-z), x^2z, x^3)$: a plane $x=0$ with an embedded line $x=y-z = 0$ with a further embedded point at the origin.
$$ \begin{Bmatrix} (V(x), & 1), \\ (V(x,y-z), & \partial_x), \\ (V(x,y,z), & \partial_x^2) \end{Bmatrix} $$

Macaulay2, version 1.20
i1 : needsPackage "NoetherianOperators";
i2 : R = QQ[x,y];
i3 : I = ideal(x*y-x*z,x^2*z,x^3);
i4 : differentialPrimaryDecomposition I
o4 = {{ideal x, {| 1 |}}, {ideal (y - z, x), {| dx |}}, {ideal (z, y, x), {| dx^2 |}}}
o4 : List
J. Chen, Y. Cid-Ruiz, M. Härkönen, R. Krone, and A. Leykin, Noetherian operators in Macaulay2, 2021. arXiv:2101.01002.
Behind the scenes
- Algorithms rely on linear algebra over residue fields $\kappa(\pp)$, where $\mathfrak{\pp} \in \operatorname{Ass}(I)$ Cid-Ruiz,Sturmfels (2022)
- Some numerical approaches possible Chen, H., Krone, Leykin (2022)
- Embedded primes? Ongoing work
- What do operations on ideal look like dually? H. (2022) (PhD. thesis)
- Intersection
- Sum
- Saturation, colons
- Elimination
- Even more minimal representation? Socles, module generators... Ait El Manssour, H., Sturmfels (2021)
- Application in analysis, algebra... H., Nicklasson, Raiță(2021)
Learning PDE solutions
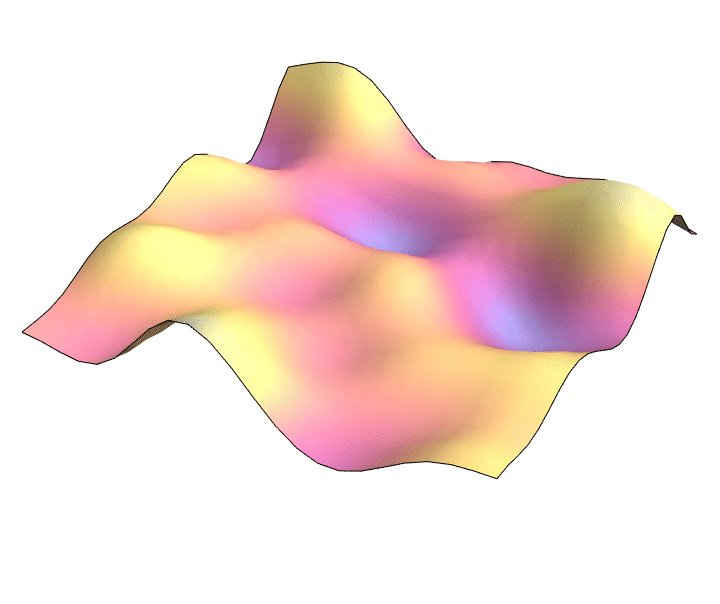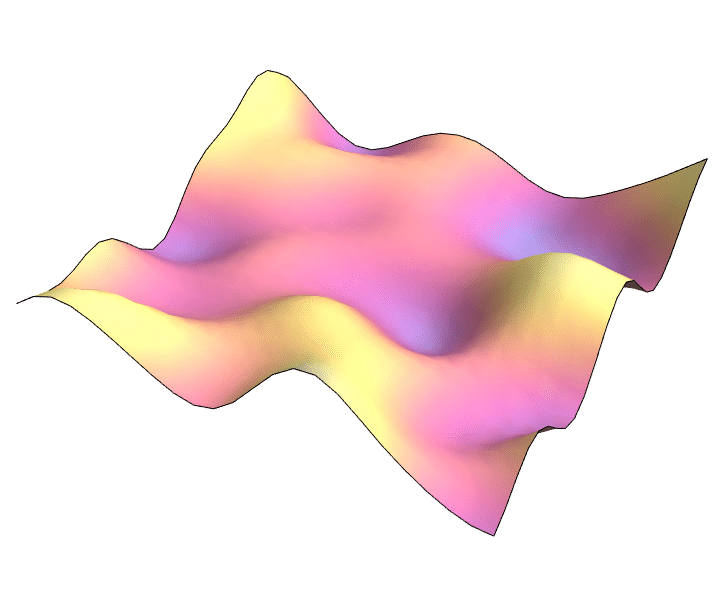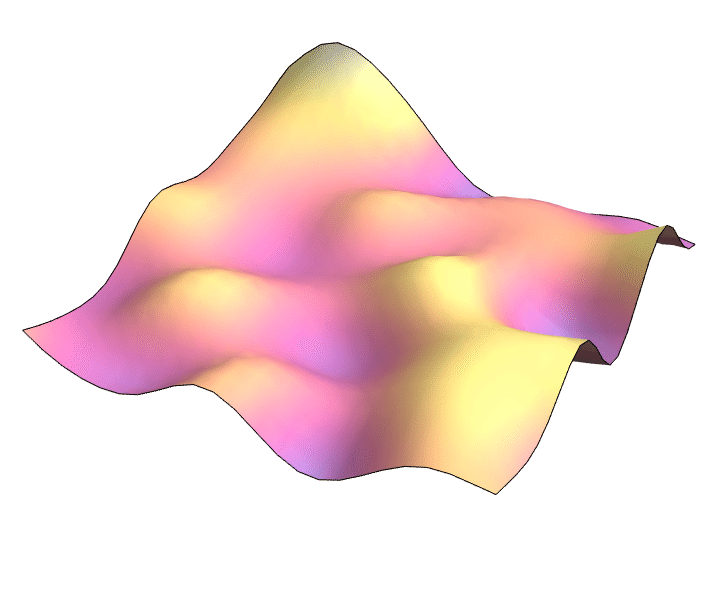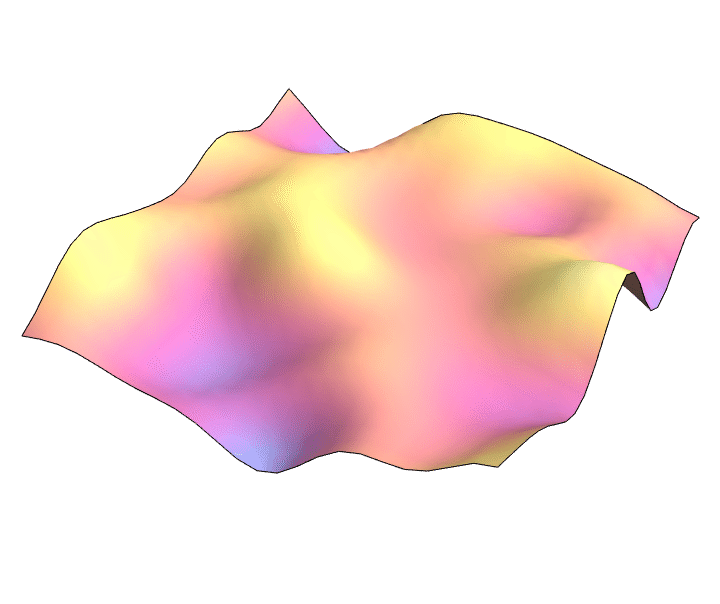
$ \partial_t^2 u = \Delta u $
Joint with Markus Lange-Hegermann (TH OWL) and Bogdan Raiță (SNS Pisa)
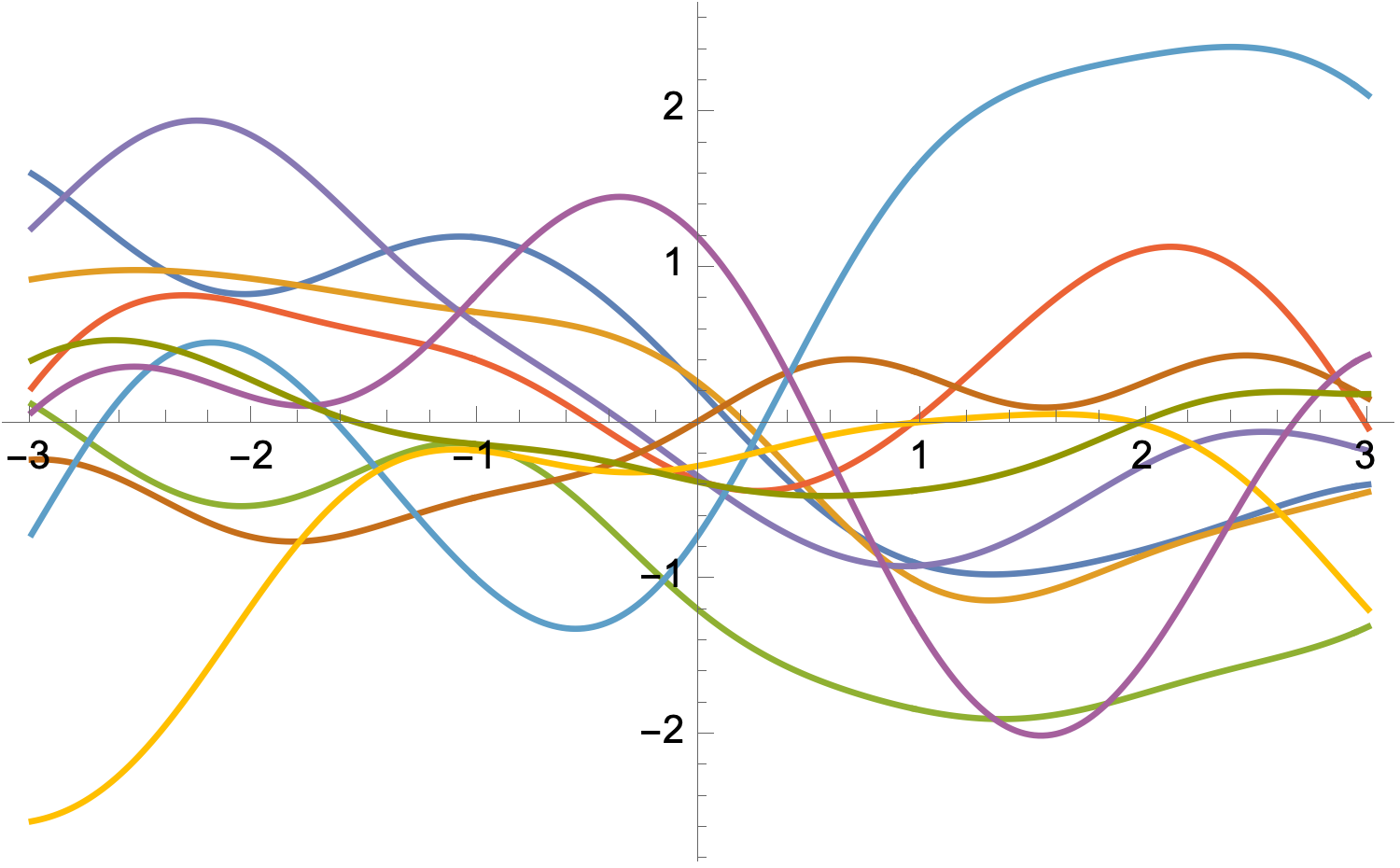
Gaussian Processes
Continuous analogue of Gaussian random variables
$ f(\mathbf{z}) \sim \operatorname{GP}(\mu(\mathbf{z}), k(\mathbf{z},\mathbf{z}')) $
$ \mathbb{E}[f(\mathbf{z})] = \mu(\mathbf{z}) $
$ \operatorname{Cov}(f(\mathbf{z}), f(\mathbf{z}')) = k(\mathbf{z},\mathbf{z}') $
Gaussian Processes
Continuous analogue of Gaussian random variables
$ f(\mathbf{z}) \sim \operatorname{GP}(\mu(\mathbf{z}), k(\mathbf{z},\mathbf{z}')) $
$ \mathbb{E}[f(\mathbf{z})] = \mu(\mathbf{z}) $
$ \operatorname{Cov}(f(\mathbf{z}), f(\mathbf{z}')) = k(\mathbf{z},\mathbf{z}') $
Gaussian Processes
Continuous analogue of Gaussian random variables
$ f(\mathbf{z}) \sim \operatorname{GP}(\mu(\mathbf{z}), k(\mathbf{z},\mathbf{z}')) $
$ \mathbb{E}[f(\mathbf{z})] = \mu(\mathbf{z}) $
$ \operatorname{Cov}(f(\mathbf{z}), f(\mathbf{z}')) = k(\mathbf{z},\mathbf{z}') $

$ \Rightarrow $
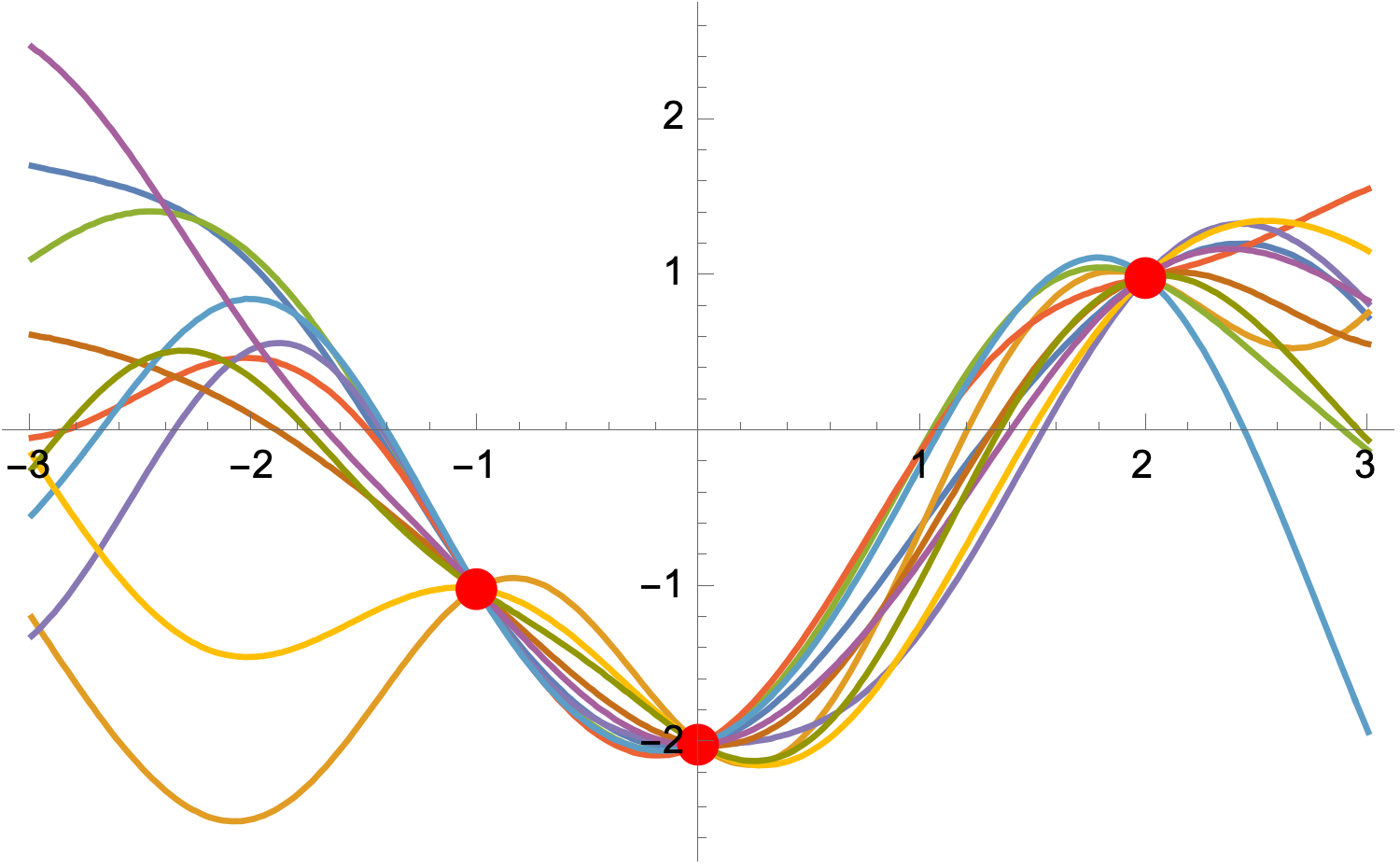
Gaussian Processes
Continuous analogue of Gaussian random variables
$ f(\mathbf{z}) \sim \operatorname{GP}(\mu(\mathbf{z}), k(\mathbf{z},\mathbf{z}')) $
$ \mathbb{E}[f(\mathbf{z})] = \mu(\mathbf{z}) $
$ \operatorname{Cov}(f(\mathbf{z}), f(\mathbf{z}')) = k(\mathbf{z},\mathbf{z}') $

$ \Rightarrow $

$ k(z,z') = e^{-\frac{(z-z')^2}{2}}, \qquad \mu(x) = 0 $
Gaussian processes are linear (in many (nice) ways)
If $ f(\mathbf{z}) \sim \operatorname{GP}(\mu(\mathbf{z}), k(\mathbf{z},\mathbf{z}')) $
then $ \partial_z f(\mathbf{z}) \sim \operatorname{GP}(\partial_z \mu(\mathbf{z}), \partial_z \partial_{z'}k(\mathbf{z},\mathbf{z}')) $
then $ A(\partial_z) f(\mathbf{z}) \sim \operatorname{GP}(A(\partial_z) \mu(\mathbf{z}), A(\partial_z)A(\partial_{z'})k(\mathbf{z},\mathbf{z}')) $
Gaussian processes are linear (in many (nice) ways)
If $ f(\mathbf{z}) \sim \operatorname{GP}(\mu(\mathbf{z}), k(\mathbf{z},\mathbf{z}')) $
then $ A(\partial_z) f(\mathbf{z}) \sim \operatorname{GP}(A(\partial_z) \mu(\mathbf{z}), A(\partial_z)A(\partial_{z'})k(\mathbf{z},\mathbf{z}')) $
Realizations of $\operatorname{GP}(\mu, k)$ satisfy $A(\partial_z)$ if
- $ A\mu = 0 $$\quad\mu = 0$
- $ A(\partial_{z})A(\partial_{z'})k = 0 $
Realizations of $\operatorname{GP}(\mu, k)$ satisfy $A(\partial_z)$ if
- $ A(\partial_{z})A(\partial_{z'})k = 0 $
Find a $k$ that solves the PDE $A$ in $z, z'$.
$$ k(z,z') = \int_V D(x,z)D(x,z')e^{x^T z} e^{\overline{x}^T z'} \, d\mu(x) $$
Let $x = (x_1,x_2)$, assume $V$ in Noether normal position with respect to $x_1$.
Realizations of $\operatorname{GP}(\mu, k)$ satisfy $A(\partial_z)$ if
- $ A(\partial_{z})A(\partial_{z'})k = 0 $
Find a $k$ that solves the PDE $A$ in $z, z'$.
$$ k(z,z') = \int_{\RR^d} \sum_{x \in V \colon x=(ix_1, x_2)} D(x,z)D(x,z')e^{x^T z} e^{\overline{x}^T z'} \, d\mu(x_1) $$
Let $x = (x_1,x_2)$, assume $V$ in Noether normal position with respect to $x_1$.
Realizations of $\operatorname{GP}(\mu, k)$ satisfy $A(\partial_z)$ if
- $ A(\partial_{z})A(\partial_{z'})k = 0 $
Find a $k$ that solves the PDE $A$ in $z, z'$.
$$ k(z,z') = \int_{\RR^d} \sum_{x \in V \colon x=(ix_1, x_2)} D(x,z)D(x,z')e^{x^T z} e^{\overline{x}^T z'} \, e^{-\frac{\|x_1\|^2}{2}} d\mathcal{L}(x_1) $$
Let $x = (x_1,x_2)$, assume $V$ in Noether normal position with respect to $x_1$.
Realizations of $\operatorname{GP}(\mu, k)$ satisfy $A(\partial_z)$ if
- $ A(\partial_{z})A(\partial_{z'})k = 0 $
Find a $k$ that solves the PDE $A$ in $z, z'$.
$$ k(z,z') = \int_{\RR^d} \sum_{x \in V \colon x=(ix_1, x_2)} D(x,z)D(x,z')e^{x^T z} e^{\overline{x}^T z'} \, e^{-\frac{\|x_1\|^2}{2}} d\mathcal{L}(x_1) $$
Let $x = (x_1,x_2)$, assume $V$ in Noether normal position with respect to $x_1$.
$$ A = 0 \Rightarrow k(z,z') = \int_{\RR^n} e^{i(z-z')^T x} e^{-\frac{x^2}{2}} \, d\mathcal{L}(x) \\ \qquad\quad = \sqrt{2\pi}^n e^{-\frac{(z-z')^2}{2}} $$
$$ k(z,z') = \int_{\RR^d} \sum_{x \in V \colon x=(ix_1, x_2)} D(x,z)D(x,z')e^{x^T z} e^{\overline{x}^T z'} \, e^{-\frac{\|x_1\|^2}{2}} d\mathcal{L}(x_1) $$
In practice: Monte-Carlo + numerical solving
1D heat equation: $\partial_t = \partial_x^2$
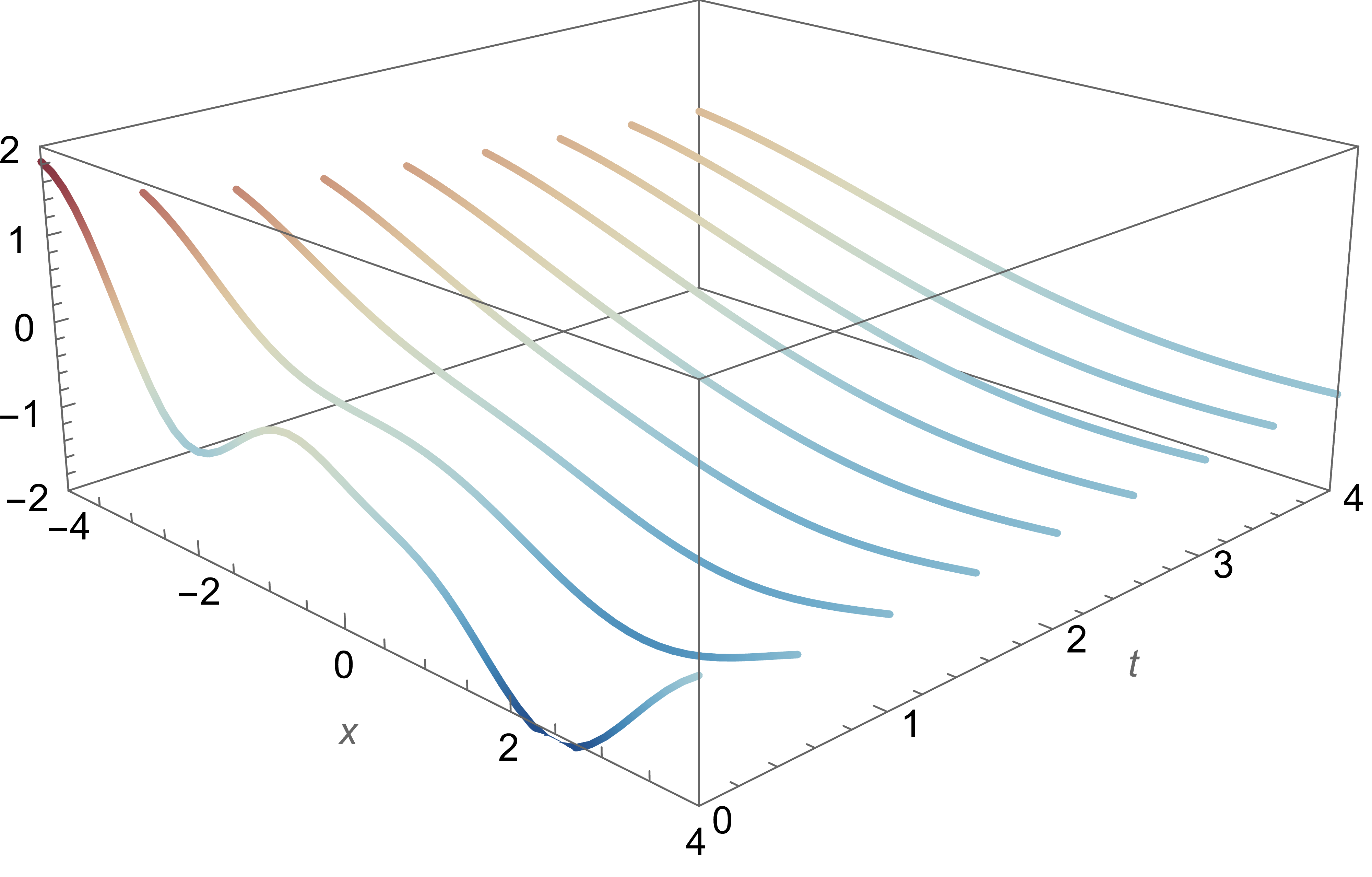
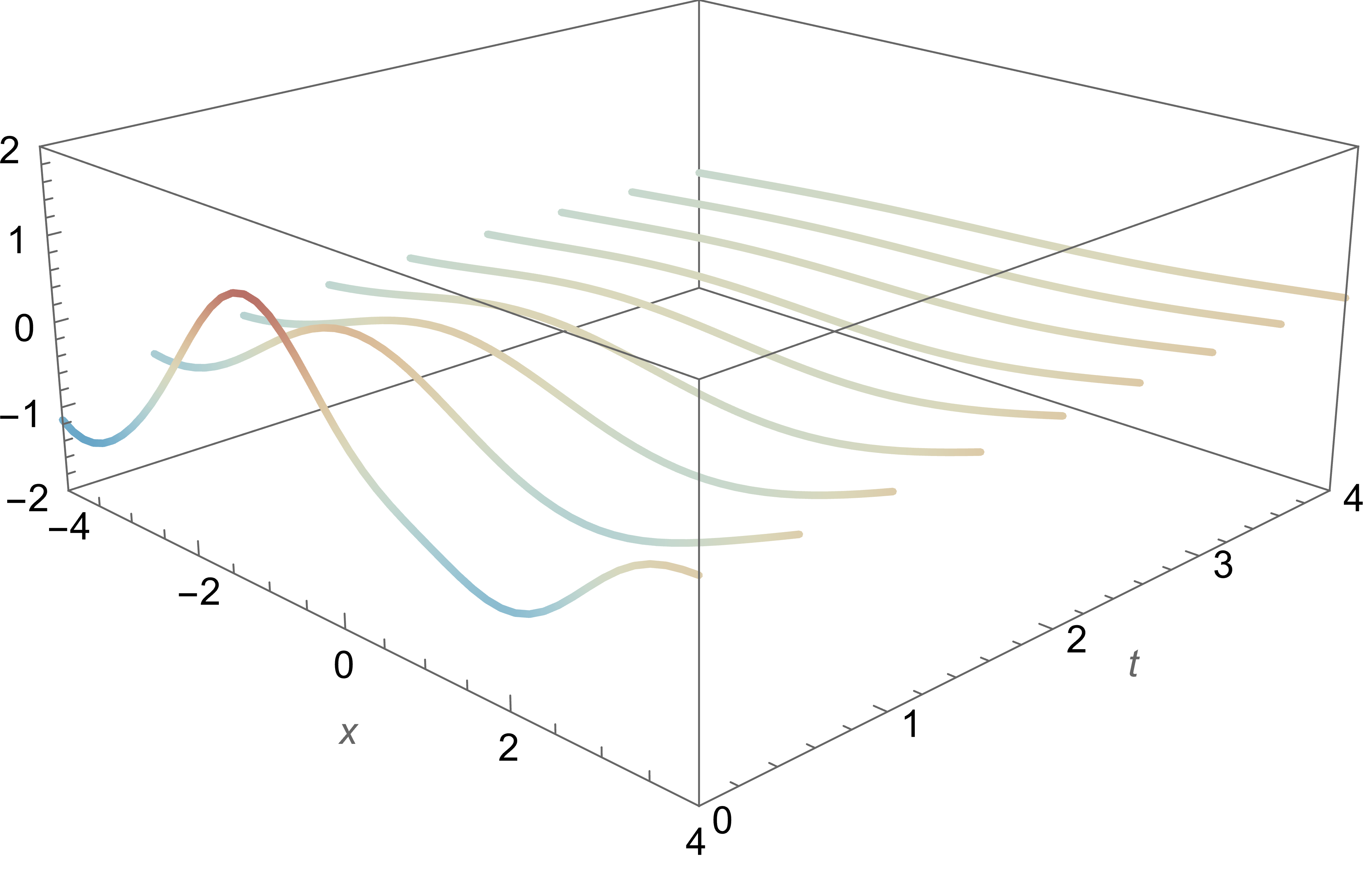
$$ k(z,z') = \int_{\RR^d} \sum_{x \in V \colon x=(ix_1, x_2)} D(x,z)D(x,z')e^{x^T z} e^{\overline{x}^T z'} \, e^{-\frac{\|x_1\|^2}{2}} d\mathcal{L}(x_1) $$
In practice: Monte-Carlo + numerical solving
1D heat equation: $\partial_t = \partial_x^2$
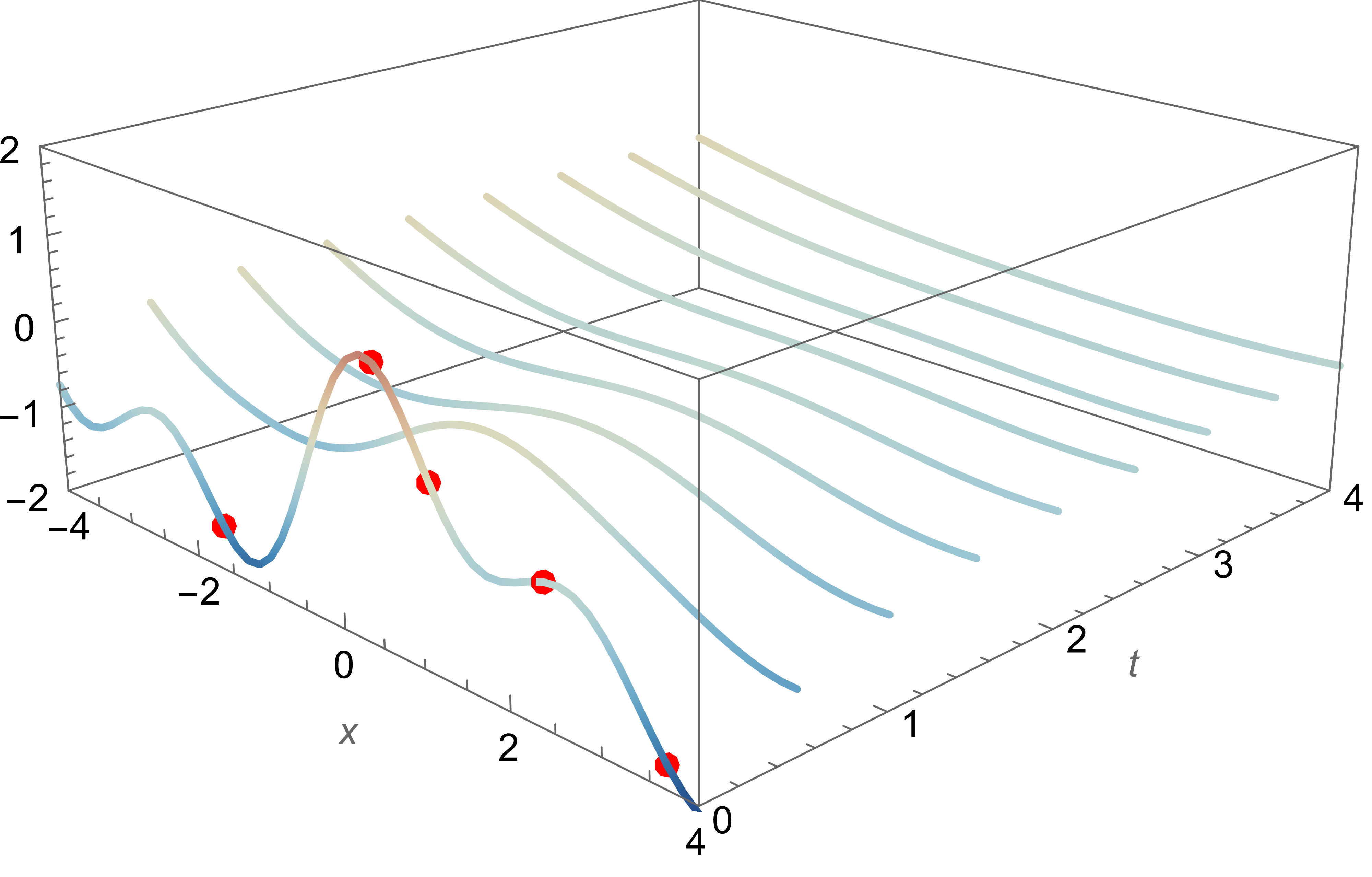
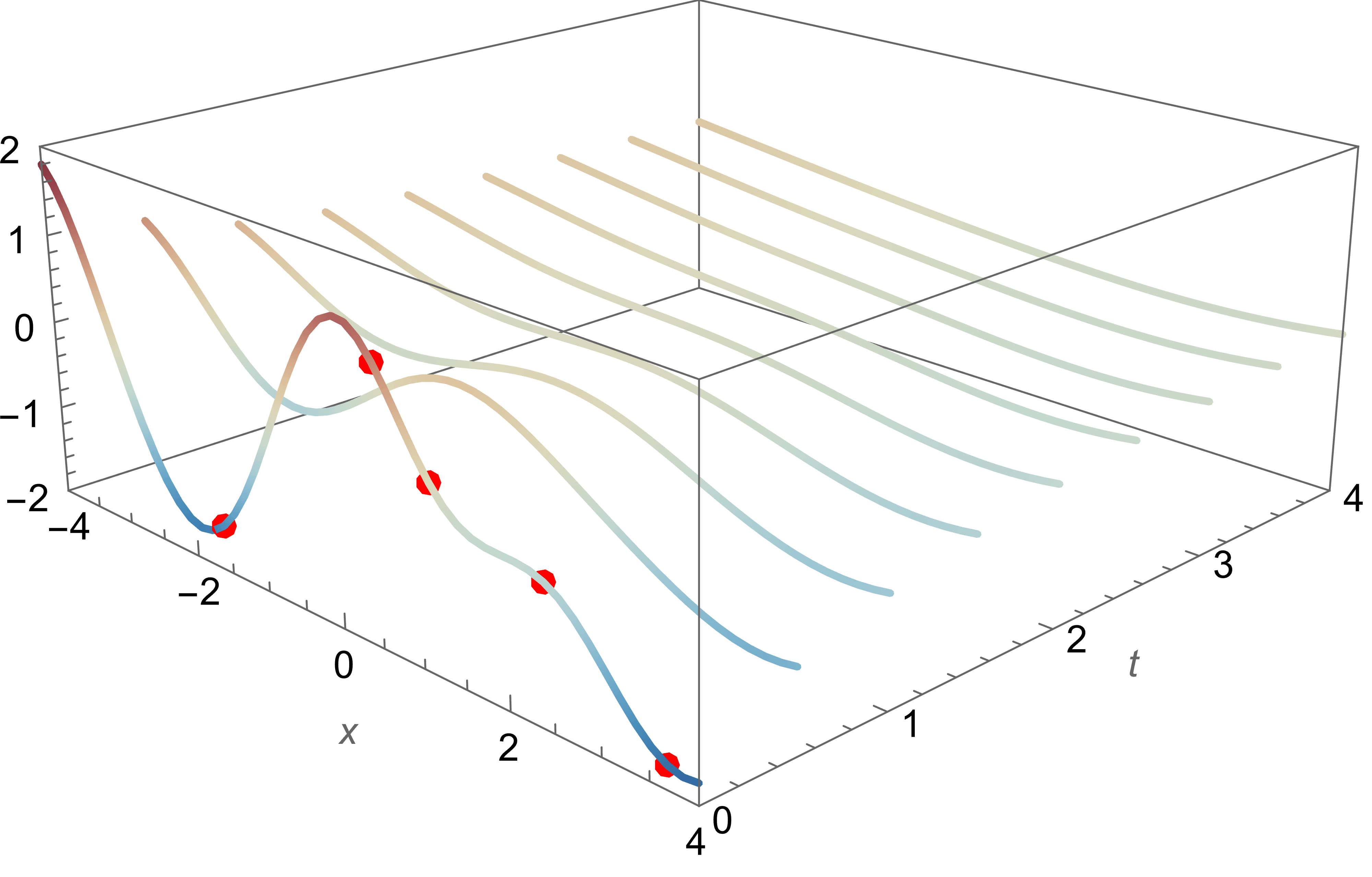
2D wave equation: $\partial_t^2 = \partial_x^2 + \partial_y^2$
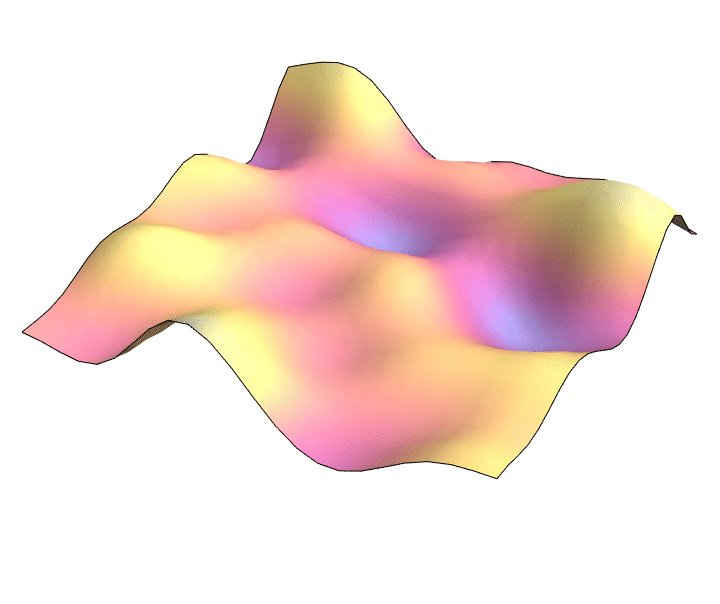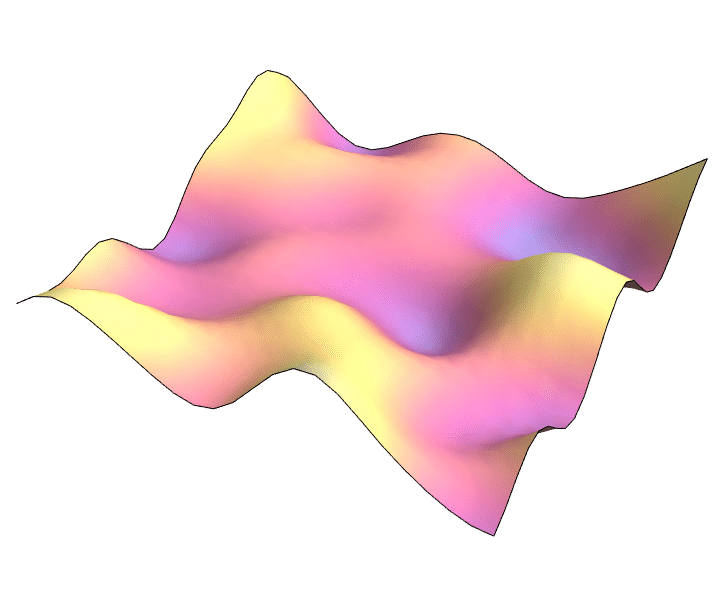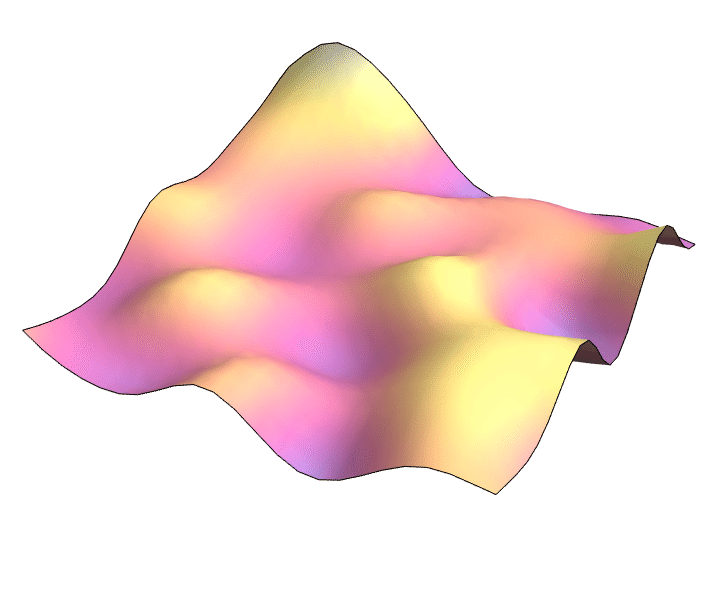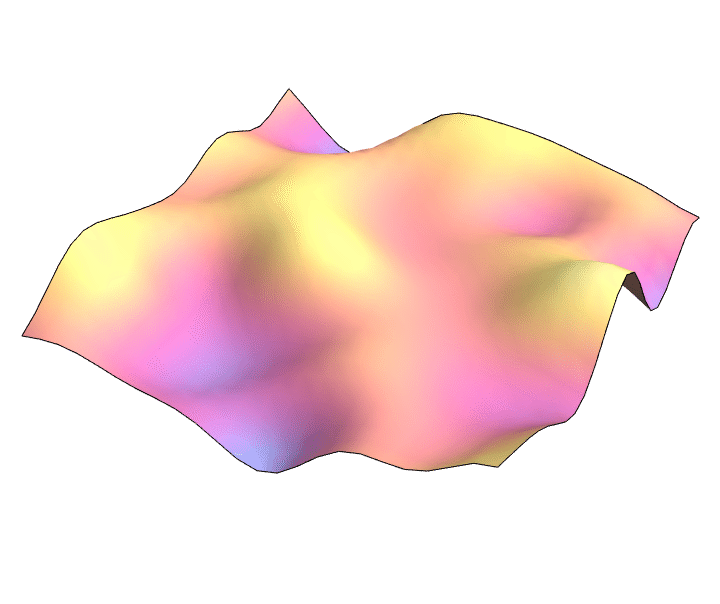
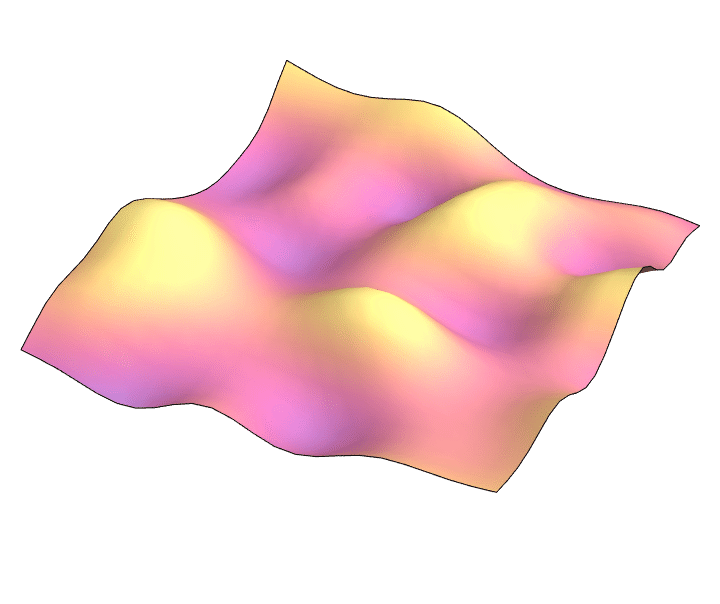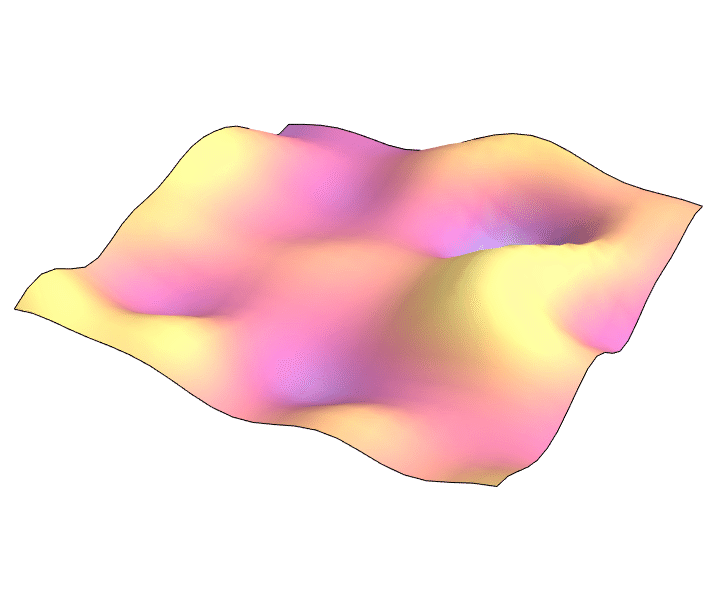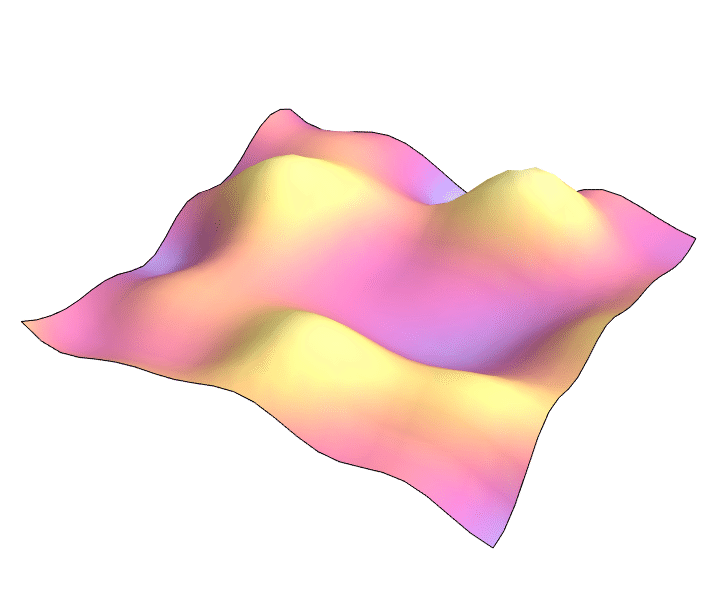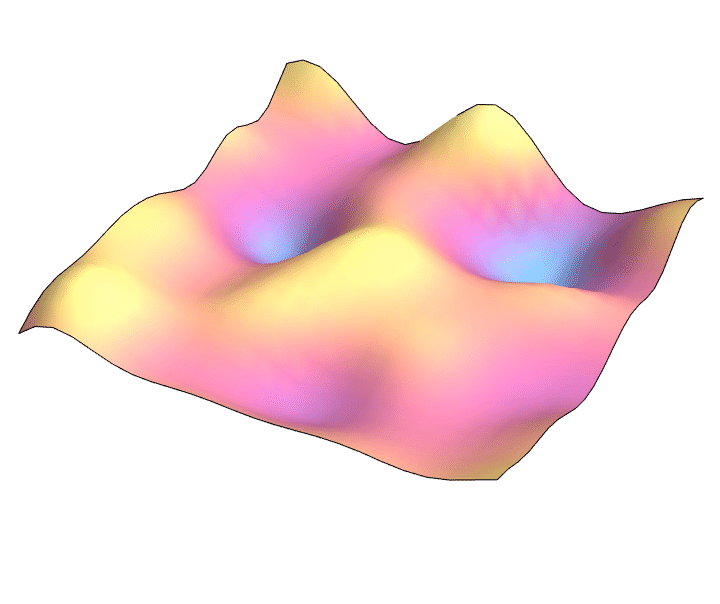

2D wave equation: $\partial_t^2 = \partial_x^2 + \partial_y^2$
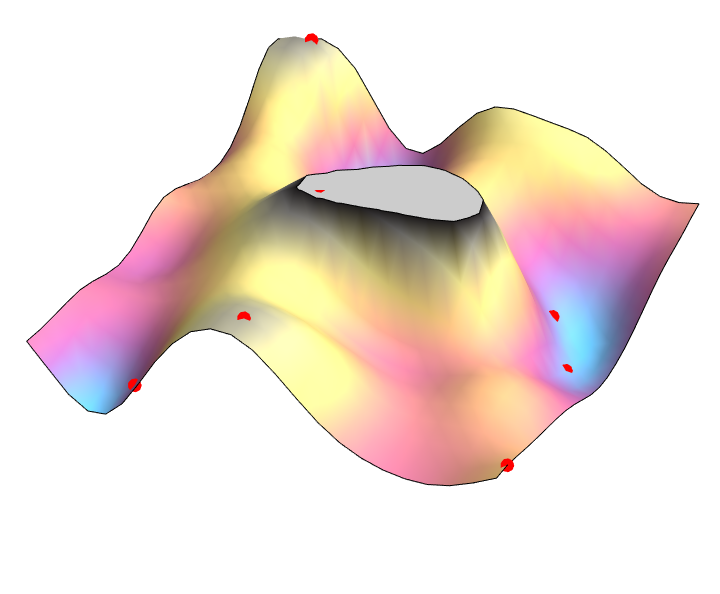
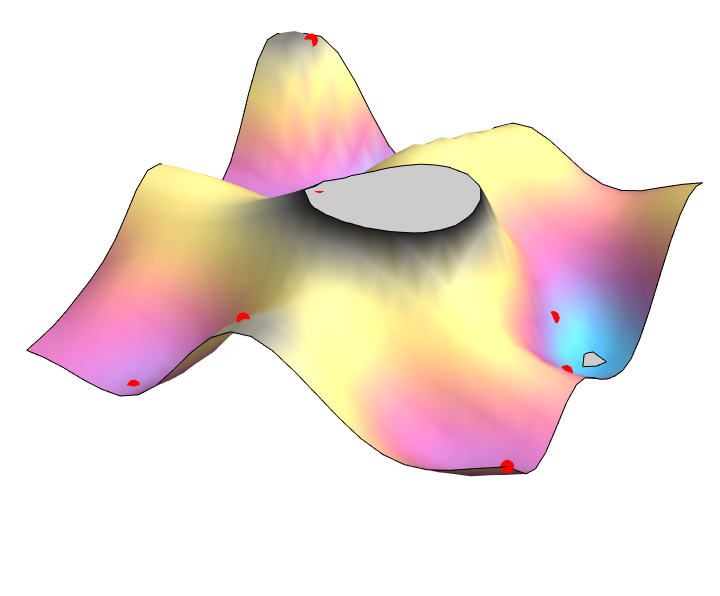
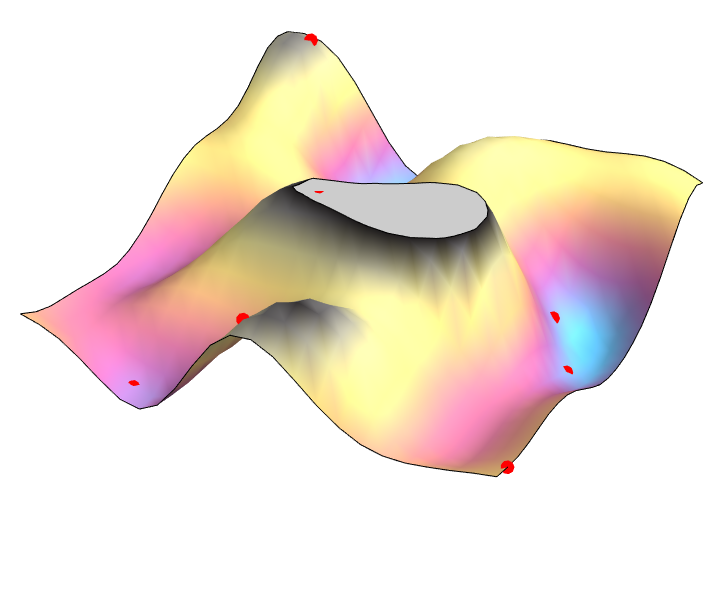
2D wave equation: $\partial_t^2 = \partial_x^2 + \partial_y^2$
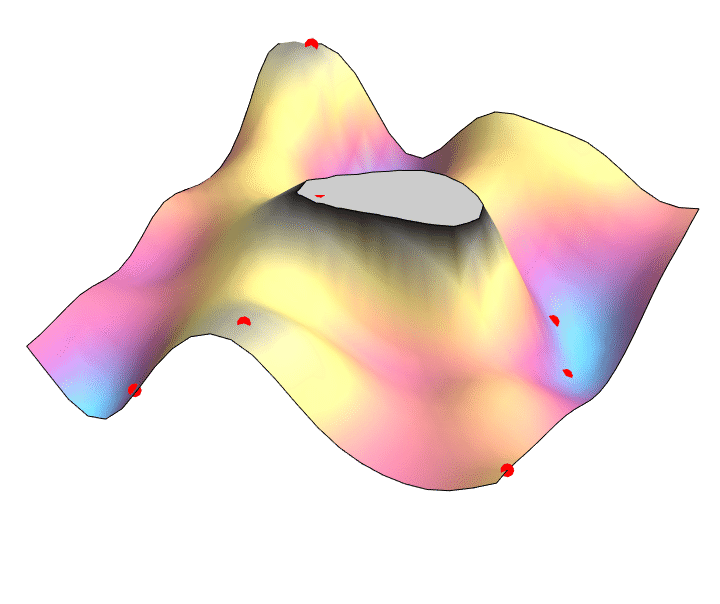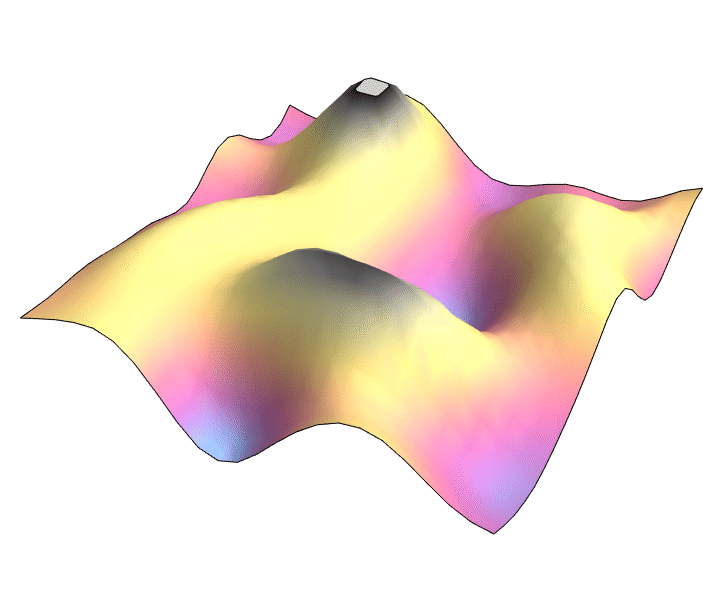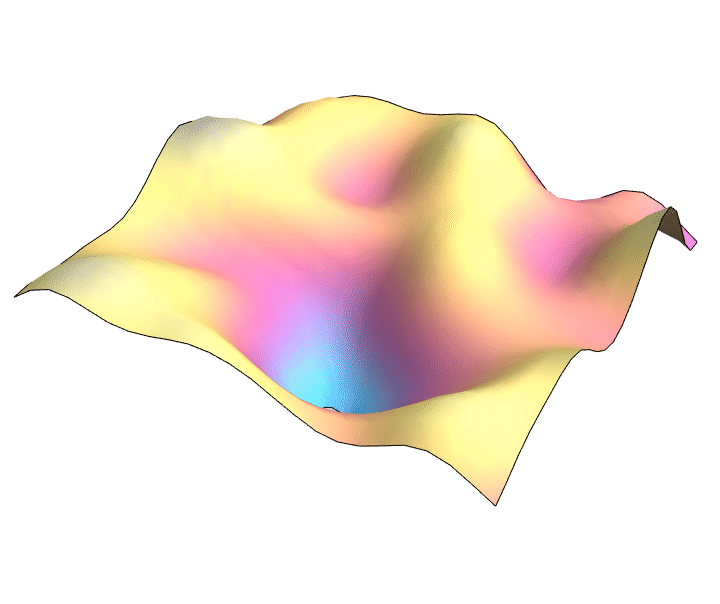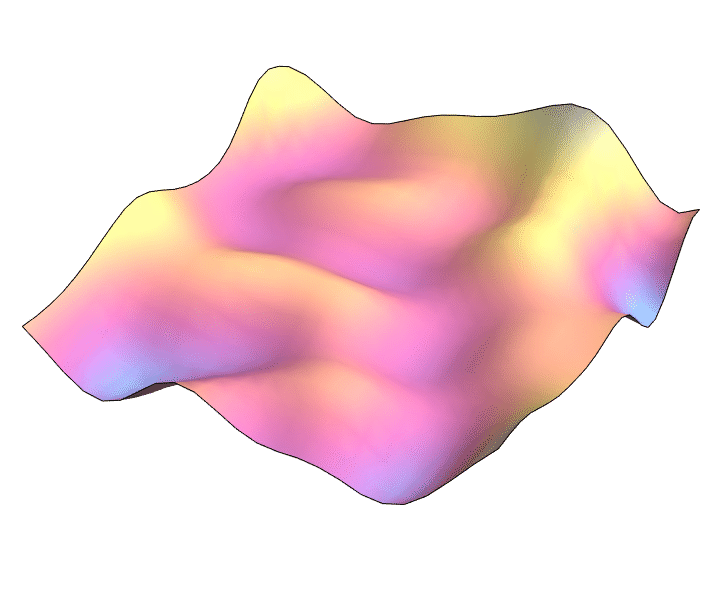
Thank you!
Homework: Solve the PDE
Hint:
needsPackage "NoetherianOperators";
viewHelp(solvePDE)Thank you!
